Démonstration de la conjecture de Legendre
16 messages
- Page 1 sur 1
Démonstration de la conjecture de Legendre
Bonjour,
Le mathématicien Adrien Legendre a conjecturé la présence d'au moins un nombre premier entre deux carrés consécutifs. J'ai réalisé une démonstration de cette conjecture. Elle est accessible à http://vixra.org/pdf/1407.0203v1.pdf
J'apprécierais recevoir des commentaires quant à cette démonstration.
Merci!
Le mathématicien Adrien Legendre a conjecturé la présence d'au moins un nombre premier entre deux carrés consécutifs. J'ai réalisé une démonstration de cette conjecture. Elle est accessible à http://vixra.org/pdf/1407.0203v1.pdf
J'apprécierais recevoir des commentaires quant à cette démonstration.
Merci!
rere a écrit:Bonjour,
Le mathématicien Adrien Legendre a conjecturé la présence d'au moins un nombre premier entre deux carrés consécutifs. J'ai réalisé une démonstration de cette conjecture. Elle est accessible à http://vixra.org/pdf/1407.0203v1.pdf
J'apprécierais recevoir des commentaires quant à cette démonstration.
Merci!
j'ai des doutes sur la véracité de la preuve du lemme.
J'ai calculé
à revoir donc...
wserdx a écrit:j'ai des doutes sur la véracité de la preuve du lemme.
J'ai calculéalors que ta formule donne 2*11-1=21.
à revoir donc...
Bonjour,
Merci d'avoir pris le temps de faire une première lecture de cette démonstration.
J'observe une erreur dans votre calcul puisque vous n'utilisez pas les bonnes valeurs des nombres premiers. Il faut savoir que p6=13 et p7=17. En prenant ces valeurs pour p7 et p6 ma formule donne Lp7= 2*p6 - 1 = 2*13-1 = 25. On peut voir aussi qu'en pratique le résultat est bien 25 lorsqu'on exécute l'algorithme.
Au plaisir de poursuivre cette discussion!
Bonjour,
j'ai retiré mon premier post, j'avais fait mes calculs un peu trop vite... :mur:
Je les ai refait jusqu'à p=19 et ça concorde. :we:
Ceci dit, la démonstration du lemme n'est pas claire pour moi: je ne comprends pas le calcul de la valeur . Peux-tu détailler ce point?
. Peux-tu détailler ce point?
Sinon, si tout se tient, ce serait un beau résultat!
j'ai retiré mon premier post, j'avais fait mes calculs un peu trop vite... :mur:
Je les ai refait jusqu'à p=19 et ça concorde. :we:
Ceci dit, la démonstration du lemme n'est pas claire pour moi: je ne comprends pas le calcul de la valeur
Sinon, si tout se tient, ce serait un beau résultat!
Salut,
Quand tu écris "La plus longue suite de nombres composés consécutifs dont chacun des termes est
divisible par au moins un des nombres premiers 2, 3, 5, , pi contient (2* pi-1) 1
nombres composés."
Tu veux majorer la taille de la suite où tu affirme l'existence d'une telle suite ?
Parce que cela voudrait dire qu'il existe une suite de 3 nombre composés consécutifs dont chacun est divisible par deux..
Ou alors je n'ai pas bien compris le lemme..
Edit : j'avais pas vu que c'étais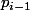 :mur: au temps pour moi, et désolé pour cette intervention inutile
:mur: au temps pour moi, et désolé pour cette intervention inutile
Quand tu écris "La plus longue suite de nombres composés consécutifs dont chacun des termes est
divisible par au moins un des nombres premiers 2, 3, 5, , pi contient (2* pi-1) 1
nombres composés."
Tu veux majorer la taille de la suite où tu affirme l'existence d'une telle suite ?
Parce que cela voudrait dire qu'il existe une suite de 3 nombre composés consécutifs dont chacun est divisible par deux..
Ou alors je n'ai pas bien compris le lemme..
Edit : j'avais pas vu que c'étais
wserdx a écrit:Bonjour,
j'ai retiré mon premier post, j'avais fait mes calculs un peu trop vite... :mur:
Je les ai refait jusqu'à p=19 et ça concorde. :we:
Ceci dit, la démonstration du lemme n'est pas claire pour moi: je ne comprends pas le calcul de la valeur. Peux-tu détailler ce point?
Sinon, si tout se tient, ce serait un beau résultat!
Bonjour,
Le calcul
Cordialement
rere
lulubibi28 a écrit:A quoi servirait en pratique cet algorithme en informatique ?
Bonjour,
Cet algorithme est construit uniquement pour démontrer le lemme. Toutefois on pourrait bien sûr le programmer afin d'obtenir des suites de nombres divisibles seulement par un ou plusieurs des nombres premiers de la suite 2,3,5,7,11,...pi.
Je ne vois pas d'utilité pratique aujourd'hui, mais il faut se rappeler qu'en mathématique il arrive souvent que l'utilité soit perçue beaucoup plus tard que le développement de la théorie.
Salutations!
adrien69 a écrit:Là personnellement je crois que tu l'as mal compris (je ne me prononcerai pas sur le reste, ce n'est pas le genre de maths qui m'intéressent).
Si l'on considère le lemme comme étant bon, a priori la plus longue suite de nombres composés tous divisibles par 2 est de taille 1.
Edit : (c'est quoi ?)
Bonjour,
Les nombres premiers, par convention, sont numérotés à partir de
D'après ce que j'ai lu et compris, le lemme m'a l'air intéressant (et en tout cas semble vrai quand on fait des test sur des petits nombres premiers).
J'aimerais cependant faire 2/3 remarques (ou poser des questions).
1. Je comprends mal l'explication de l'algorithme. Tu dis qu'il faut mettre le 3 dans une case proche du centre et pas encore occupée par un 2. Comment définis-tu mathématiquement "proche du centre" ? Est-ce que tu peux prendre un nombre pair de cases et mettre ton 3 sur la case centrale et ça fonctionne toujours, ou c'est un peu plus "au feeling" ?
En gros, je me demande ce que tu entends mathématiquement par "près du centre" ?
2. Il me semble (corrige moi si je me trompe), que ce que tu démontres dans le lemme c'est que avec ton algorithme, tu peux créer une suite de nombre composés [...] (J'abrège l'énoncé du lemme par flemme de tout taper), de longueur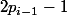 . Mais tu ne prouves pas que ton algorithme est optimal. Si ça se trouve, il existe des algorithme plus efficaces qui permettent de construire des suites plus longues.
. Mais tu ne prouves pas que ton algorithme est optimal. Si ça se trouve, il existe des algorithme plus efficaces qui permettent de construire des suites plus longues.
Donc comment démontres-tu que ton algorithme est optimal ? (Parce qu'il ne me semble pas l'avoir vu)
3. C'est une remarque mathématique (pas une question) qui mintrigue.
Je vais supposer ton lemme vrai, donc la plus longue suite [... ] vaut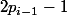 .
.
En ce qui me concerne, je sais construire une suite de nombre composés consécutifs dont la longueur est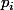 . Comment ? En considérant la suite
. Comment ? En considérant la suite 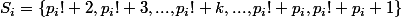 .
.
Sauf erreur de ma part, cette suite contient bien nombre composés consécutifs dont chacun des termes est divisible soit par 2, soit par 3,... soit par
nombre composés consécutifs dont chacun des termes est divisible soit par 2, soit par 3,... soit par  .
.
Ce que je peux en conclure, c'est que est inférieur à la plus longue suite de nombre composés consécutifs [...]
est inférieur à la plus longue suite de nombre composés consécutifs [...]
J'en conclus, en admettant ton lemme :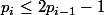 .
.
Ce qui est un résultat intéressant aussi...
Car sachant que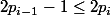 , on pourrait en déduire que "il existe toujours un nombre premier entre
, on pourrait en déduire que "il existe toujours un nombre premier entre  et
et 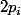 "
"
Bref, c'est intéressant, mais il faudrait être sûr que ton lemme soit correct.
J'aimerais cependant faire 2/3 remarques (ou poser des questions).
1. Je comprends mal l'explication de l'algorithme. Tu dis qu'il faut mettre le 3 dans une case proche du centre et pas encore occupée par un 2. Comment définis-tu mathématiquement "proche du centre" ? Est-ce que tu peux prendre un nombre pair de cases et mettre ton 3 sur la case centrale et ça fonctionne toujours, ou c'est un peu plus "au feeling" ?
En gros, je me demande ce que tu entends mathématiquement par "près du centre" ?
2. Il me semble (corrige moi si je me trompe), que ce que tu démontres dans le lemme c'est que avec ton algorithme, tu peux créer une suite de nombre composés [...] (J'abrège l'énoncé du lemme par flemme de tout taper), de longueur
Donc comment démontres-tu que ton algorithme est optimal ? (Parce qu'il ne me semble pas l'avoir vu)
3. C'est une remarque mathématique (pas une question) qui mintrigue.
Je vais supposer ton lemme vrai, donc la plus longue suite [... ] vaut
En ce qui me concerne, je sais construire une suite de nombre composés consécutifs dont la longueur est
Sauf erreur de ma part, cette suite contient bien
Ce que je peux en conclure, c'est que
J'en conclus, en admettant ton lemme :
Ce qui est un résultat intéressant aussi...
Car sachant que
Bref, c'est intéressant, mais il faudrait être sûr que ton lemme soit correct.
Lamaths a écrit:D'après ce que j'ai lu et compris, le lemme m'a l'air intéressant (et en tout cas semble vrai quand on fait des test sur des petits nombres premiers).
J'aimerais cependant faire 2/3 remarques (ou poser des questions).
1. Je comprends mal l'explication de l'algorithme. Tu dis qu'il faut mettre le 3 dans une case proche du centre et pas encore occupée par un 2. Comment définis-tu mathématiquement "proche du centre" ? Est-ce que tu peux prendre un nombre pair de cases et mettre ton 3 sur la case centrale et ça fonctionne toujours, ou c'est un peu plus "au feeling" ?
En gros, je me demande ce que tu entends mathématiquement par "près du centre" ?
2. Il me semble (corrige moi si je me trompe), que ce que tu démontres dans le lemme c'est que avec ton algorithme, tu peux créer une suite de nombre composés [...] (J'abrège l'énoncé du lemme par flemme de tout taper), de longueur. Mais tu ne prouves pas que ton algorithme est optimal. Si ça se trouve, il existe des algorithme plus efficaces qui permettent de construire des suites plus longues.
Donc comment démontres-tu que ton algorithme est optimal ? (Parce qu'il ne me semble pas l'avoir vu)
3. C'est une remarque mathématique (pas une question) qui mintrigue.
Je vais supposer ton lemme vrai, donc la plus longue suite [... ] vaut.
En ce qui me concerne, je sais construire une suite de nombre composés consécutifs dont la longueur est. Comment ? En considérant la suite
.
Sauf erreur de ma part, cette suite contient biennombre composés consécutifs dont chacun des termes est divisible soit par 2, soit par 3,... soit par
.
Ce que je peux en conclure, c'est queest inférieur à la plus longue suite de nombre composés consécutifs [...]
J'en conclus, en admettant ton lemme :.
Ce qui est un résultat intéressant aussi...
Car sachant que, on pourrait en déduire que "il existe toujours un nombre premier entre
et
"
Bref, c'est intéressant, mais il faudrait être sûr que ton lemme soit correct.
Bonjour,
Merci d'avoir lu cette démonstration avec autant d'attention.
1. Je veux dire par "proche du centre" à peu près au centre car cela est sans importance, c'est juste pour utiliser au mieux l'espace disponible dans le schéma. Le nombre de cases doit être simplement assez grand pour contenir la suite éventuelle, mais de toute façon s'il manque des cases on peut toujours en ajouter à gauche ou à droite.
2. Si vous connaissez un algorithme plus efficace qui permette de construire des suites plus longues j'aimerais bien le connaître.
3. Je connais cette technique pour obtenir une suite de nombres consécutifs sans aucun nombre premier. Il vous manque un terme au début et il y en un de trop à la fin. Par exemple pour une suite de 3 nombres on aura 3!+1, 3!+2, 3!+3, mais pas 3!+4. Aussi, pour ce qui est de la présence d'un nombre premier entre n et 2n, c'est le postulat de Bertrand et le mathématicien Paul Erdos en a fait une démonstration déjà.
Mes salutations!
rere a écrit:Bonjour,
Merci d'avoir lu cette démonstration avec autant d'attention.
1. Je veux dire par "proche du centre" à peu près au centre car cela est sans importance, c'est juste pour utiliser au mieux l'espace disponible dans le schéma. Le nombre de cases doit être simplement assez grand pour contenir la suite éventuelle, mais de toute façon s'il manque des cases on peut toujours en ajouter à gauche ou à droite.
2. Si vous connaissez un algorithme plus efficace qui permette de construire des suites plus longues j'aimerais bien le connaître.
3. Je connais cette technique pour obtenir une suite de nombres consécutifs sans aucun nombre premier. Il vous manque un terme au début et il y en un de trop à la fin. Par exemple pour une suite de 3 nombres on aura 3!+1, 3!+2, 3!+3, mais pas 3!+4. Aussi, pour ce qui est de la présence d'un nombre premier entre n et 2n, c'est le postulat de Bertrand et le mathématicien Paul Erdos en a fait une démonstration déjà.
Mes salutations!
Merci pour ces réponses.
2. Pour l'algorithme plus efficace, je n'en connais pas. Seul problème : ce n'est pas parce que je n'en connais pas qu'il n'en n'existe pas.
Pour être plus clair : Ce que tu as démontré, c'est que l'algorithme proposé permet de mettre en évidence des suites de
On peut alors affirmer que la plus longue suite de nombres composés consécutifs est de longueur supérieure à
Par contre, pour affirmer que la longueur de cette plus longue suite est exactement
Mettons-nous d'accord, je ne dis pas que ton algorithme n'est pas optimal (à vrai dire, je n'en sais rien, et l'intuition me pousserait à dire qu'il est optimal), le soucis c'est que rien ne le prouve.
3. Justement, je n'ai pas mis le terme
Par contre je ne connaissais pas le postulat de Bertrand, merci de m'avoir dit ce nom.
rere a écrit:Bonjour,
Le calculmesure la différence de longueur entre la suite de nombres du premier schéma et la suite de nombres du deuxième schéma. Cette différence étant la même du côté gauche et du côté droit. Pour saisir cette différence il importe de noter que le premier schéma correspond à p indice n tandis que le deuxième correspond à p indice n+1. La première suite se termine du côté droit avec le nombre premier p indice n-1, alors que la deuxième suite se termine avec p indice n. Le delta est la différence entre ces deux derniers nombres premiers.
Cordialement
rere
Bonsoir,
Si je comprends mieux, il me semble que tu utilises le fait que ton algorithme calcule la plus longue suite ayant les propriétés souhaitées? C'est cela? Si oui, il en manque la preuve.
Peux-tu confirmer?
De manière générale, essaie de réécrire ton papier sous forme de propositions suivies de leur démonstration.
Bien à toi.
Bonjour,
Pour être un peu constructif, je reformule ton "algorithme".
Soit la plus petite solution au problème des restes chinois:
la plus petite solution au problème des restes chinois:
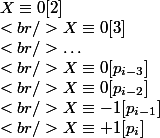
(Il est bien connu que ce problème admet une plus petite solution, et il est facile de la calculer et toutes les autres solutions se déduisent en ajoutant un multiple de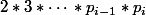 )
)
Par construction de , il est facile de voir que tous les nombres
, il est facile de voir que tous les nombres
compris entre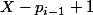 et
et 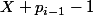 ont au moins un diviseur parmi
ont au moins un diviseur parmi 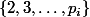
et que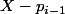 et
et 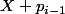 n'en n'ont pas.
n'en n'ont pas.
Mais rien ne dit que cet intervalle est le plus long...
A démontrer donc.
Pour être un peu constructif, je reformule ton "algorithme".
Soit
(Il est bien connu que ce problème admet une plus petite solution, et il est facile de la calculer et toutes les autres solutions se déduisent en ajoutant un multiple de
Par construction de
compris entre
et que
Mais rien ne dit que cet intervalle est le plus long...
A démontrer donc.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
