Conjecture Riemann

par **Archytas** » 05 Nov 2012, 21:34

Salut, je voulais savoir une petite précision on dit que la fonction zéta: (z->somme des 1/(n^(x+i*y)) avec z=x+i*y) de Riemann s'annule pour une valeur de x=1/2 c'est bien ça ? J'ai essayé de simuler cette suite et même s'il est vrai que pour certain y la suite semble converger vers 0, ils sont très peu :(. Est-ce que j'ai mal compris cette conjecture ? Elle est pas vraie pour tout y ?! Je ne comprends pas et ça me prend la tête !
C'est pas pressé et je compte absolument pas essayer de résoudre cette conjecture juste la comprendre comme elle semble être très importante dans les maths. Si quelqun voulait bien m'éclairer :) !

par **DamX** » 07 Nov 2012, 11:06

Archytas a écrit:Salut, je voulais savoir une petite précision on dit que la fonction zéta: (z->somme des 1/(n^(x+i*y)) avec z=x+i*y) de Riemann s'annule pour une valeur de x=1/2 c'est bien ça ? J'ai essayé de simuler cette suite et même s'il est vrai que pour certain y la suite semble converger vers 0, ils sont très peu . Est-ce que j'ai mal compris cette conjecture ? Elle est pas vraie pour tout y ?! Je ne comprends pas et ça me prend la tête !
C'est pas pressé et je compte absolument pas essayer de résoudre cette conjecture juste la comprendre comme elle semble être très importante dans les maths. Si quelqun voulait bien m'éclairer !

Hello,

Non ce n'est pas vrai pour tout y. La conjecture de Riemann stipule que tous les zéros non triviaux de zêta sont situés sur la droite x=1/2, mais absolument pas que zêta s'annule sur toute la droite (ce qui est faux et explique pourquoi tu ne converges pas vers 0..)

[url]http://fr.wikipedia.org/wiki/Hypothèse_de_Riemann[/url]

Damien

par **kazeriahm** » 07 Nov 2012, 11:18

Salut

la fonction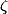

(zeta) de Riemann est définie pour

par

.

En utilisant des outils d'analyse complexe (la théorie des fonctions définies et à valeurs dans le corps des nombres complexes, très riche), on montre qu'il existe un unique prolongement analytique (analytique signifie, pour simplifier, de classe

) à

.

La conjecture de Riemann énonce que les zéros non triviaux de la fonction ainsi obtenus se trouvent tous sur la droite

. Ceci-dit on ne peut pas calculer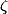

sur cette droite grâce à la formule initiale (la série n'est pas convergente si

, hormis pour quelques valeurs de

).

par **Archytas** » 07 Nov 2012, 11:28

Ah oui, d'accord, c'est beaucoup plus complexe que ce que j'avais entendu (sans faire de mauvais jeux de mots) ! Je vous remercie pour vos réponse, même si du coup c'est beaucoup moins clair quoique beaucoup plus vrai. Juste c'est quoi les zéros dis "triviaux" et "non triviaux" ?

par **kazeriahm** » 07 Nov 2012, 13:41

Quand on prolonge par analyticité la fonction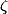

sur

, on ne connait pas de belle formule pour calculer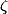

"explicitement" (comme la somme des 1/n^z), parcontre on sait que la fonction ainsi obtenue vérifie une équation dite fonctionelle (voir la page wikipédia de la fonction zeta).

On vérifie facilement grâce à cette équation fonctionelle que les entiers pairs négatifs sont des zéros de zeta, et ces zéros sont appelés zéros triviaux.

La conjecture de Riemann stipule que les zéros non triviaux sont tous situés sur la fameuse droite critique.

par **Archytas** » 07 Nov 2012, 18:38

D'accord !! Mais pour z=1 on connait déjà cette fonction !? C'est la série harmonique non ?? Je vais voir ça pour les zéros triviaux ça me fera un petit exercice !

par **kazeriahm** » 07 Nov 2012, 23:21

Archytas a écrit:D'accord !! Mais pour z=1 on connait déjà cette fonction !? C'est la série harmonique non ?? Je vais voir ça pour les zéros triviaux ça me fera un petit exercice !

Bah pour z=1 oui on retrouve la série harmonique, qui diverge. Tu comprends bien pourquoi

n'est pas défini, et ne "peut pas être défini par continuité/analyticité"

par **Archytas** » 07 Nov 2012, 23:28

kazeriahm a écrit:Bah pour z=1 oui on retrouve la série harmonique, qui diverge. Tu comprends bien pourquoi n'est pas défini, et ne "peut pas être défini par continuité/analyticité"

Pas définie ? Par continuité je comprends pas parce qu'elle est parfaitement définie puisqu'aucun dénominateur est nul quand à l'analyticité on a pas encore vu ces notions il me semble :/ et pour z=-1 par exemple elle diverge aussi et est calculable puisque zéta(-1)=n*(n+1)/2 !? Oulala j'ai raté une marche (voire l'escalier tout entier) ! Désolé pour ma lenteur d'esprit !

par **kazeriahm** » 08 Nov 2012, 08:35

Archytas a écrit:Pas définie ? Par continuité je comprends pas parce qu'elle est parfaitement définie puisqu'aucun dénominateur est nul quand à l'analyticité on a pas encore vu ces notions il me semble :/ et pour z=-1 par exemple elle diverge aussi et est calculable puisque zéta(-1)=n*(n+1)/2 !? Oulala j'ai raté une marche (voire l'escalier tout entier) ! Désolé pour ma lenteur d'esprit !

C'est toi qui parle de série harmonique ! J'imagine que c'est quelque chose que tu connais. Que vaut la série harmonique ?

Qui est n dans ta définition de zeta(-1) ? C'est n'importe quoi ! Encore une fois, on ne peut zeta(z) grâce à la somme des 1/n^z QUE si Re z > 1, ce qui n'est pas le cas de z=-1 !

par **Archytas** » 08 Nov 2012, 10:50

kazeriahm a écrit:C'est toi qui parle de série harmonique ! J'imagine que c'est quelque chose que tu connais. Que vaut la série harmonique ?

Qui est n dans ta définition de zeta(-1) ? C'est n'importe quoi ! Encore une fois, on ne peut zeta(z) grâce à la somme des 1/n^z QUE si Re z > 1, ce qui n'est pas le cas de z=-1 !

Ahh d'accord, je comprends mieux, oui cette série est la somme des inverse ! ça veut dire que pour Re(z)=1.00000000001 elle converge ? C'est étrange ! Hum, d'accord merci beaucoup et merci pour ta patience (: !

Conjecture Riemann

conjecture Riemann

Qui est en ligne