Besoin d'aide sur une Conjecture
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 19:45
par Dinozzo13 » 06 Sep 2010, 19:45
Bonsoir, j'aurai besoin d'aide pour trouver une formule donnant les valeurs suivantes :
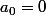
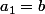
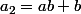
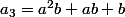
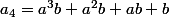
Une idée ?
J'avais pensé à
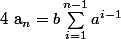
mais ça ne marche pas, c'est surtout le
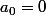
qui me bloque
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Sep 2010, 19:47
par Doraki » 06 Sep 2010, 19:47
Pourquoi est-ce que a0 = 0 te bloque ?
u(n+1) = a*u(n) + b ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 19:48
par Dinozzo13 » 06 Sep 2010, 19:48
nam justement, je dois exprimer a_n en fonction de a, b et n :cry:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Sep 2010, 19:50
par Nightmare » 06 Sep 2010, 19:50
Salut,
la suite
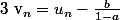
est géométrique, avec ça tu devrais pouvoir conclure.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 06 Sep 2010, 19:51
par Arnaud-29-31 » 06 Sep 2010, 19:51
Salut Dinozzo,
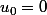
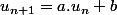
Suite arithmético-géométrique : tu peux sans soucis exprimer

en fonction de a,b et n.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 19:53
par Dinozzo13 » 06 Sep 2010, 19:53
Salut Nigntmare !
:hum: tu veux dire
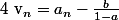
est géométrique ?
Comment as-tu choisis la suite v pour y arriver ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 19:54
par Dinozzo13 » 06 Sep 2010, 19:54
Arnaud-29-31 a écrit:Salut Dinozzo,
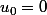
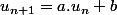
Suite arithmético-géométrique : tu peux sans soucis exprimer

en fonction de a,b et n.
Ben explique moi alors parce que là je vois pas

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Sep 2010, 19:56
par girdav » 06 Sep 2010, 19:56
Tu peux dans un premier temps chercher

tel que la suite
}_{n\in \mathbb{N}})
soit géométrique.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 19:57
par Dinozzo13 » 06 Sep 2010, 19:57
Ok, mais à quoi cela va-t-il nous mener ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Sep 2010, 19:59
par Nightmare » 06 Sep 2010, 19:59
Eh bien on aura
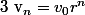
donc
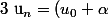r^{n}-\alpha)
:happy3:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 06 Sep 2010, 20:01
par Arnaud-29-31 » 06 Sep 2010, 20:01
Et bien tu as une suite arithmético-géométrique :
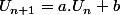
Tu appliques la méthode systématique :
On cherche

tel que la suite (
)
définie par
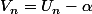
soit géométrique.


 + b + \alpha.(a-1))
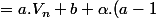)
Donc
)
est géométrique si
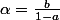
: c'est ce que te proposait nightmare.
On a donc
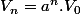
Soit donc
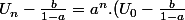)
Finalement,
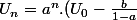 + \frac{b}{1-a})
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 20:04
par Dinozzo13 » 06 Sep 2010, 20:04
Oulala c'est la basard tout ça, reprenons lentement il est tard xD
Déjà d'où il sort votre

? ou
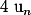
?
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 06 Sep 2010, 20:04
par Mathusalem » 06 Sep 2010, 20:04
Et par exemple :
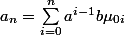
ou

est une sorte d'inverse du delta de Kronecker, à savoir
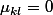
si k = l,
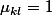
si


C'est solide, ça
EDIT: On peut remplacer

par
^2)
Je suis ouvert à quiconque m'explique pourquoi cette formule vaut vraiment pas grand chose, à savoir :
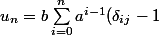^2)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 06 Sep 2010, 20:06
par Arnaud-29-31 » 06 Sep 2010, 20:06
Le

c'est ton

(on l'a noté u parce que tu as déja un a !)
Ensuite je l'ai mis en majuscule car en minuscule on confond facilement le u et le v
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 20:07
par Dinozzo13 » 06 Sep 2010, 20:07
Mathusalem a écrit:delta de Kronecker
Pas encore vu xD
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Sep 2010, 20:07
par Nightmare » 06 Sep 2010, 20:07
Mon u(n) est celui de Doraki, tu n'as jamais fait ça au lycée? La méthode, sans être à apprendre par coeur, est normalement rencontrée en 1ère ou Term.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 20:08
par Dinozzo13 » 06 Sep 2010, 20:08
Ok je vais regarder tout ça de plus près merci à tous :++:
Je repasserai demain au cas où :+++:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 20:10
par Dinozzo13 » 06 Sep 2010, 20:10
Nightmare a écrit:Mon u(n) est celui de Doraki, tu n'as jamais fait ça au lycée? La méthode, sans être à apprendre par coeur, est normalement rencontrée en 1ère ou Term.
Ben 'faut croire que non :triste:
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 06 Sep 2010, 20:13
par gigamesh » 06 Sep 2010, 20:13
Mathusalem a écrit:Et par exemple :
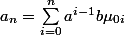
ou

est une sorte d'inverse du delta de Kronecker, à savoir
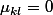
si k = l,
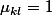
si


C'est solide, ça
Ou tout simplement
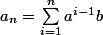
le cas n=0 se ramène à une somme vide...
Mais je pense qu'on demande une expression plus explicite ;
* si a=1 alors
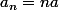
* sinon
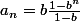
avec la formule sur la somme des termes d'une suite géométrique (et la formule marche aussi pour n=0)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Sep 2010, 20:21
par Dinozzo13 » 06 Sep 2010, 20:21
gigamesh a écrit:Ou tout simplement
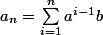
le cas n=0 se ramène à une somme vide...
Donc pour n=0 on a bien a_0=0 ???!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
est une sorte d'inverse du delta de Kronecker, à savoir
si k = l,
si