Un regard sur la conjecture de Collatz
76 messages
- Page 3 sur 4 - 1, 2, 3, 4
Re: un regard sur la conjecture de Collatz
Mea maxima culpa, j'ai fait des erreurs et je m'en excuse, je vais tenter pour la dernière fois de les réparer et serai très attentif à tout commentaires.
Voila mon dernier post :
Une suite de Collatz commence par un nombre entier positif non nul x(1), et la suite de Collatz est définie par les deux règles:
1- si un nombre x(i) est pair le nombre suivant x(i+1) = x(i)/2
2- si un nombre x(i) est impair le nombre suivant x(i+1)=3*x(i)+1
En fait la règle 1- peut s'écrire: si le nombre x(i) est pair il est de la forme (2*n-1)*2^k, n et k > 0, et on le divise par 2^k pour obtenir le nombre impair x(i+1) = 2*n-1.
Si x(i) est pair on défini donc x(i+1) impair = x(i)/2^k.
Ainsi tout nombre entier pair positif non nul x(i) a un successeur unique entier impair non nul x(i+1) et tout nombre entier impair x(i) a un successeur unique pair x(i+1).Tout nombre impair a donc un successeur impair unique ainsi que tout nombre pair a un successeur pair unique, aucun nombre pair ou impair multiple de 3 ne peut être un successeur, les nombres multiples de 3 ne peuvent être qu'en première position x(1).
On peut s'intéresser uniquement aux nombres impairs x(j), pour cela il faut définir comment les nombres impairs se précèdent dans une suite de Collatz puisqu'on a déjà défini comment ils de succèdent .
Tout nombre impair x(j) = ((6*n-5)*4^k-1)/3 ou x(j) = (2*(6*n-1)*4^(k-1)-1)/3
pour n de 1 à N et pour k de 1 à K, N et K aussi grand qu'on veut.
Tout nombre impair x(j) < ((6*N-5)*4^K-1)/3 est représenté une fois et une fois seulement pour un couple n, k donné par x(j) = ((6*n-5)*4^k-1)/3 ou x(j) = (2*(6*n-1)*4^(k-1)-1)/3.
Pour tout nombre impair x(1) = ((6*N-5)*4^K-1)/3, on a x(2) = 6*N-5.
Pour tout nombre impair x(1) = (2*(6*N-1)*4^(K-1)-1)/3, on a x(2) = 6*N-1.
Tout nombres impairs x(j) est de la forme 6*n-5 ou 6*n-1.
Donc tout nombre impair x(j) de la forme 6*n-5 aura pour prédécesseurs possibles:
x(j-1) = (x(i)*4^k-1)/3 avec k > 0 de 1 à K, si (x(i)*4^k-1)/3 est multiple de 3 alors x(1) = (x(i)*4^k-1)/3.
Et tout nombre impair x(j) de la forme 6*n-1 aura pour prédécesseurs possibles:
x(j-1) = (2*x(j)*4^(k-1)-1)/3 avec k > 0 de 1 à K, si (2*x(j)*4^(k-1)-1)/3 est multiple de 3 alors x(1) = (2*x(j)*4^(k-1)-1)/3.
Il est donc possible partant de x(j) de calculer tout x(j+1-i) possible pour i de 1 à j et il est évident que la suite x(j), x(j-1), x(j-2), ..., x(j-50), ..., x(3), x(2), x(1) est croissante avec quelques valeurs x(j-k) < x(j-k+1), la preuve en a était faîte par Tomas Oliveira e Silva qui a prouvé la validité de la conjecture de Collatz pour tout nombre < 91*2^50 soit une nombre de 17 chiffres 102456891522678784, ce qui précède apporte la preuve que la conjecture peut être vérifiée pour tout nombre aussi grand soit-il puisque partant de 1 on peut définir tout les x(j) possibles jusqu'à x(1) aussi grand que l'on veut, toute suite de Collatz se termine donc par 1 puis le cycle trivial.
Rappelons qu'un nombre impair x(j) < ((6*N-5)*4^K-1)/3 est représenté une fois et une fois seulement pour un couple n, k donné par ((6*n-5)*4^k-1)/3 ou (2*(6*n-1)*4^(k-1)-1)/3 et que tout nombre impair non multiple de 3 est représenté par 6*n-5 ou 6*n-1, de tous les nombres impairs 1 est le seul qui pour un couple n, k donne le même résultat pour les deux formules ((6*n-5)*4^k-1)/3 et 6*n-5, ((6*1-5)*4-1)/3 = 1 et 6*1-5 = 1 ce qui explique le cycle trivial, 1 est le seul nombre impair qui peut être à la fois sont prédécesseur et son successeur.
Aucun autre nombre impair que 1 peut se répéter dans une suite de Collatz puisqu'on a montrer que tout nombre impair successeur est différent de sont prédécesseur 1 excepté.
Voila mon dernier post :
Une suite de Collatz commence par un nombre entier positif non nul x(1), et la suite de Collatz est définie par les deux règles:
1- si un nombre x(i) est pair le nombre suivant x(i+1) = x(i)/2
2- si un nombre x(i) est impair le nombre suivant x(i+1)=3*x(i)+1
En fait la règle 1- peut s'écrire: si le nombre x(i) est pair il est de la forme (2*n-1)*2^k, n et k > 0, et on le divise par 2^k pour obtenir le nombre impair x(i+1) = 2*n-1.
Si x(i) est pair on défini donc x(i+1) impair = x(i)/2^k.
Ainsi tout nombre entier pair positif non nul x(i) a un successeur unique entier impair non nul x(i+1) et tout nombre entier impair x(i) a un successeur unique pair x(i+1).Tout nombre impair a donc un successeur impair unique ainsi que tout nombre pair a un successeur pair unique, aucun nombre pair ou impair multiple de 3 ne peut être un successeur, les nombres multiples de 3 ne peuvent être qu'en première position x(1).
On peut s'intéresser uniquement aux nombres impairs x(j), pour cela il faut définir comment les nombres impairs se précèdent dans une suite de Collatz puisqu'on a déjà défini comment ils de succèdent .
Tout nombre impair x(j) = ((6*n-5)*4^k-1)/3 ou x(j) = (2*(6*n-1)*4^(k-1)-1)/3
pour n de 1 à N et pour k de 1 à K, N et K aussi grand qu'on veut.
Tout nombre impair x(j) < ((6*N-5)*4^K-1)/3 est représenté une fois et une fois seulement pour un couple n, k donné par x(j) = ((6*n-5)*4^k-1)/3 ou x(j) = (2*(6*n-1)*4^(k-1)-1)/3.
Pour tout nombre impair x(1) = ((6*N-5)*4^K-1)/3, on a x(2) = 6*N-5.
Pour tout nombre impair x(1) = (2*(6*N-1)*4^(K-1)-1)/3, on a x(2) = 6*N-1.
Tout nombres impairs x(j) est de la forme 6*n-5 ou 6*n-1.
Donc tout nombre impair x(j) de la forme 6*n-5 aura pour prédécesseurs possibles:
x(j-1) = (x(i)*4^k-1)/3 avec k > 0 de 1 à K, si (x(i)*4^k-1)/3 est multiple de 3 alors x(1) = (x(i)*4^k-1)/3.
Et tout nombre impair x(j) de la forme 6*n-1 aura pour prédécesseurs possibles:
x(j-1) = (2*x(j)*4^(k-1)-1)/3 avec k > 0 de 1 à K, si (2*x(j)*4^(k-1)-1)/3 est multiple de 3 alors x(1) = (2*x(j)*4^(k-1)-1)/3.
Il est donc possible partant de x(j) de calculer tout x(j+1-i) possible pour i de 1 à j et il est évident que la suite x(j), x(j-1), x(j-2), ..., x(j-50), ..., x(3), x(2), x(1) est croissante avec quelques valeurs x(j-k) < x(j-k+1), la preuve en a était faîte par Tomas Oliveira e Silva qui a prouvé la validité de la conjecture de Collatz pour tout nombre < 91*2^50 soit une nombre de 17 chiffres 102456891522678784, ce qui précède apporte la preuve que la conjecture peut être vérifiée pour tout nombre aussi grand soit-il puisque partant de 1 on peut définir tout les x(j) possibles jusqu'à x(1) aussi grand que l'on veut, toute suite de Collatz se termine donc par 1 puis le cycle trivial.
Rappelons qu'un nombre impair x(j) < ((6*N-5)*4^K-1)/3 est représenté une fois et une fois seulement pour un couple n, k donné par ((6*n-5)*4^k-1)/3 ou (2*(6*n-1)*4^(k-1)-1)/3 et que tout nombre impair non multiple de 3 est représenté par 6*n-5 ou 6*n-1, de tous les nombres impairs 1 est le seul qui pour un couple n, k donne le même résultat pour les deux formules ((6*n-5)*4^k-1)/3 et 6*n-5, ((6*1-5)*4-1)/3 = 1 et 6*1-5 = 1 ce qui explique le cycle trivial, 1 est le seul nombre impair qui peut être à la fois sont prédécesseur et son successeur.
Aucun autre nombre impair que 1 peut se répéter dans une suite de Collatz puisqu'on a montrer que tout nombre impair successeur est différent de sont prédécesseur 1 excepté.
Re: un regard sur la conjecture de Collatz
Bonjour,
Essayons avec la suite inverse. On part donc de 1 :
- on ne peut qu'aller à un nombre pair, soit 2 (un nombre impair serait inférieur à 1 : impossible)
- de 2, on peut aller à toutes les puissances de 2 : 4, 8, 16, 32, ...
- de 2, on peut essayer d'aller à un nombre impair : 3n+1=2, impossible ; comme tu l'as remarqué, pour aller à un nombre impair, il faut partir d'une puissance paire de 2 : 3n+1=4, soit n=1, on retombe sur 1
- sortons de ce cycle, avec 16 (8 ne marche pas vu plus haut) ; 3n+1=16, soit n=5 ; on obtient 5
- de là, on peut aller à 10, 20, 40, ...
- cherchons un nombre impair : on ne peut pas partir de 5 car 5=2²+1 ; 3n+1=10, soit n=3
- on obtient 6, 12, 24, ..., puis on est bloqué car multiples de 3
- on repart de 40 (20 ne marche pas) : 3n+1=40, soit n=13
- etc...
Comment peux-tu être sûr qu'avec ce procédé, on va aboutir à 7 ? Quelle est la suite des nombres qui part de 1 pour aboutir à 7 ? (je dis bien : qui part de 1, pas qui part de 7). Quelle est la suite des nombres qui part de 1 pour aboutir à 13246 ? Quel est le procédé algorithmique ? (je dis bien : qui part de 1 pour aboutir à 13246)
Essayons avec la suite inverse. On part donc de 1 :
- on ne peut qu'aller à un nombre pair, soit 2 (un nombre impair serait inférieur à 1 : impossible)
- de 2, on peut aller à toutes les puissances de 2 : 4, 8, 16, 32, ...
- de 2, on peut essayer d'aller à un nombre impair : 3n+1=2, impossible ; comme tu l'as remarqué, pour aller à un nombre impair, il faut partir d'une puissance paire de 2 : 3n+1=4, soit n=1, on retombe sur 1
- sortons de ce cycle, avec 16 (8 ne marche pas vu plus haut) ; 3n+1=16, soit n=5 ; on obtient 5
- de là, on peut aller à 10, 20, 40, ...
- cherchons un nombre impair : on ne peut pas partir de 5 car 5=2²+1 ; 3n+1=10, soit n=3
- on obtient 6, 12, 24, ..., puis on est bloqué car multiples de 3
- on repart de 40 (20 ne marche pas) : 3n+1=40, soit n=13
- etc...
Comment peux-tu être sûr qu'avec ce procédé, on va aboutir à 7 ? Quelle est la suite des nombres qui part de 1 pour aboutir à 7 ? (je dis bien : qui part de 1, pas qui part de 7). Quelle est la suite des nombres qui part de 1 pour aboutir à 13246 ? Quel est le procédé algorithmique ? (je dis bien : qui part de 1 pour aboutir à 13246)
Modifié en dernier par Pseuda le 15 Aoû 2018, 13:04, modifié 1 fois.
Re: un regard sur la conjecture de Collatz
la suite inverse des impairs qui conduit au nombre pair 13246=2*6623 est donnée ci dessous,
remarquez bien qu'aucun nombre impair de cette suite apparait 2 fois et qu'aucun d'eux est multiple de 3, de plus il ne exister aucune autre suite inverse de Collatz de nombres impairs conduisant de 1 à 6623, toute suite inverse de Collatz entre 1 et tout nombre impair > 1 est unique.
En ce qui concerne l'algorithme utilisé pour l'obtenir il vous suffit d'utiliser les formules décrites dans mon post précédent, et pour 1 à 7 trop facile: 1, 5, 13, 17, 11, 7 .
1
5
53
35
23
61
325
433
577
3077
2051
1367
911
2429
1619
1079
719
479
319
425
283
377
251
167
445
593
395
263
175
233
155
103
137
91
485
323
215
143
95
253
337
449
299
797
2125
11333
7555
10073
6715
8953
47749
63665
42443
28295
18863
12575
33533
22355
14903
9935
6623
remarquez bien qu'aucun nombre impair de cette suite apparait 2 fois et qu'aucun d'eux est multiple de 3, de plus il ne exister aucune autre suite inverse de Collatz de nombres impairs conduisant de 1 à 6623, toute suite inverse de Collatz entre 1 et tout nombre impair > 1 est unique.
En ce qui concerne l'algorithme utilisé pour l'obtenir il vous suffit d'utiliser les formules décrites dans mon post précédent, et pour 1 à 7 trop facile: 1, 5, 13, 17, 11, 7 .
1
5
53
35
23
61
325
433
577
3077
2051
1367
911
2429
1619
1079
719
479
319
425
283
377
251
167
445
593
395
263
175
233
155
103
137
91
485
323
215
143
95
253
337
449
299
797
2125
11333
7555
10073
6715
8953
47749
63665
42443
28295
18863
12575
33533
22355
14903
9935
6623
Modifié en dernier par CAMI le 14 Aoû 2018, 13:46, modifié 1 fois.
Re: un regard sur la conjecture de Collatz
Quand je vous demandais comment on passe de 1 à 13246, c'était une image pour que vous réalisiez que vous ne sauriez pas déterminer le processus qui vous y conduit.
Bon, comment passe-t-on de 1 à N, N quelconque impair (pour simplifier). Quel est le processus, l'algorithme qui y conduit à coup sûr ? Pouvez-vous expliquer (dans le détail) pourquoi vous êtes allé de 1 à 5, puis de 5 à 53, etc..., pour aller à 13246 ?
Petite remarque : s'il y avait une autre suite inverse de Collatz qui mène de 1 à 6623, vous ne trouvez pas que ce serait légèrement bizarre ? Même question pour un nombre impair qui figurerait 2 fois dans la liste ? Même question pour un nombre impair multiple de 3 ?
Bon, comment passe-t-on de 1 à N, N quelconque impair (pour simplifier). Quel est le processus, l'algorithme qui y conduit à coup sûr ? Pouvez-vous expliquer (dans le détail) pourquoi vous êtes allé de 1 à 5, puis de 5 à 53, etc..., pour aller à 13246 ?
Petite remarque : s'il y avait une autre suite inverse de Collatz qui mène de 1 à 6623, vous ne trouvez pas que ce serait légèrement bizarre ? Même question pour un nombre impair qui figurerait 2 fois dans la liste ? Même question pour un nombre impair multiple de 3 ?
Re: un regard sur la conjecture de Collatz
Je n'ai aucune raison de vous donner mon algorithme mais si vous en avez la capacité vous pouvez vérifier que pour aller de 1 à 10^n-125117 pour n= 10, 100, 1000, 10000, 100000 il faut trouver respectivement 70, 865, 8724, 86595, 863697 nombre impairs, pas la place ici pour les écrire tous!
Donnez moi un nombre impair N quelconque de 100000 à 150000 chiffres et je vous adresse par message privé les quelques 800000 à 1000000 ou plus de nombres impairs de 1 à N dans la journée sur un fichier .txt
Donnez moi un nombre impair N quelconque de 100000 à 150000 chiffres et je vous adresse par message privé les quelques 800000 à 1000000 ou plus de nombres impairs de 1 à N dans la journée sur un fichier .txt
Re: un regard sur la conjecture de Collatz
"remarquez bien qu'aucun nombre impair de cette suite apparait 2 fois"
Si tel était le cas, comment pourrais tu parvenir à 6623 ? Tu aurais établi une boucle, et d'ailleurs, tu n'aurais pas pu partir de 1.
Prétendre que tu sais remonter l'algorithme pour arriver au nombre désiré est une mystification. Je te croyais "seulement " incapable de comprendre une preuve, puis de faire semblant de ne pas vouloir comprendre ce qu'on te disait, en fait c'est pis: tu affabules.
Si les symptômes persistent, il faut aller consulter.
Si tel était le cas, comment pourrais tu parvenir à 6623 ? Tu aurais établi une boucle, et d'ailleurs, tu n'aurais pas pu partir de 1.
Prétendre que tu sais remonter l'algorithme pour arriver au nombre désiré est une mystification. Je te croyais "seulement " incapable de comprendre une preuve, puis de faire semblant de ne pas vouloir comprendre ce qu'on te disait, en fait c'est pis: tu affabules.
Si les symptômes persistent, il faut aller consulter.
Re: un regard sur la conjecture de Collatz
Est ce que tu pense réellement que de "défier" d'autre personnes à trouver un contre exemple à une conjecture constitue ne serait-ce que le début d'une preuve concernant la conjecture en question ?CAMI a écrit:Donnez moi un nombre impair N quelconque de 100000 à 150000 chiffres et je vous adresse par message privé les quelques 800000 à 1000000 ou plus de nombres impairs de 1 à N dans la journée sur un fichier .txt
Perso, dans ton laïus, je ne voit toujours pas le moindre début d'argument allant dans le sens de montrer que tout nombre entier sera obtenu par tes "suites inverses". Tout ce que je vois, c'est :
- Quelques vagues calculs de congruence sans le moindre intérêt (vu qu'ils ne prouvent absolument rien concernant le fait que TOUT entier va être atteint)
- Des affirmation totalement gratuites et sans le moindre fondement du style "ce qui précède apporte la preuve que la conjecture peut être vérifiée pour tout nombre aussi grand soit-il puisque..."
- Des contre vérités flagrantes du style de "il est évident que la suite x(j), x(j-1), x(j-2), ..., x(j-50), ..., x(3), x(2), x(1) est croissante" qui, en plus, même si elles étaient vraies, ne constitueraient absolument pas la preuve que tout entier peut être obtenu par ce type de suite : La suite 1,2,4,8,16,...,2^n,... peut être "prolongée autant qu'on veut", elle est croissante et ne contient bien évidement pas TOUT les entiers.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un regard sur la conjecture de Collatz
En essayant de comprendre ton charabia, plus précisément ce morceau là :
N'a tu par exemple jamais entendu parler de la suite des nombres pairs ? de la suites des puissances de 2 ? de la suites des nombres premiers ? Dans tout ces cas là (et bien d'autres...) on a une suite (croissante) qui "prend des valeurs aussi grandes qu'on veut" mais qui bien sûr ne prend pas toutes les valeurs entières !
Ben ça donne on ne peut plus l'impression que, selon toi, le fait qu'une (ou des) suite(s) puisse(nt) prendre "des valeurs aussi grandes que l'on veut" (je te cite), ben ça signifie que la(les) suite(s) prennent toutes les valeurs entières possibles et imaginables.CAMI a écrit:Il est donc possible partant de x(j) de calculer tout x(j+1-i) possible pour i de 1 à j et il est évident que la suite x(j), x(j-1), x(j-2), ..., x(j-50), ..., x(3), x(2), x(1) est croissante avec quelques valeurs x(j-k) < x(j-k+1), la preuve en a était faîte par Tomas Oliveira e Silva qui a prouvé la validité de la conjecture de Collatz pour tout nombre < 91*2^50 soit une nombre de 17 chiffres 102456891522678784, ce qui précède apporte la preuve que la conjecture peut être vérifiée pour tout nombre aussi grand soit-il puisque partant de 1 on peut définir tout les x(j) possibles jusqu'à x(1) aussi grand que l'on veut, toute suite de Collatz se termine donc par 1 puis le cycle trivial.
N'a tu par exemple jamais entendu parler de la suite des nombres pairs ? de la suites des puissances de 2 ? de la suites des nombres premiers ? Dans tout ces cas là (et bien d'autres...) on a une suite (croissante) qui "prend des valeurs aussi grandes qu'on veut" mais qui bien sûr ne prend pas toutes les valeurs entières !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un regard sur la conjecture de Collatz
CAMI a écrit:Je n'ai aucune raison de vous donner mon algorithme
Vous avez raison. Pour vivre heureux, vivons cachés !
Re: un regard sur la conjecture de Collatz
CAMI a écrit:Je n'ai aucune raison de vous donner mon algorithme
Voyons, son algorithme on l' a bien deviné: il part du nombre N, calcule la suite finie qui s'arrête à 1.
Ensuite il écrit la suite à l'envers. (désolé d'avoir trahit le secret).
Re: un regard sur la conjecture de Collatz
aviateur a écrit:Voyons, son algorithme on l' a bien deviné: il part du nombre N, calcule la suite finie qui s'arrête à 1.
Ensuite il écrit la suite à l'envers. (désolé d'avoir trahit le secret).
 Il fallait quelqu'un pour le dire. Merci @aviateur, j'ai bien ri.
Il fallait quelqu'un pour le dire. Merci @aviateur, j'ai bien ri.Re: un regard sur la conjecture de Collatz
Si ce que vous dîtes est vrai vous faîtes la preuve que la conjecture est démontrée !
Re: un regard sur la conjecture de Collatz
nodgim a écrit:Si les symptômes persistent, il faut aller consulter.
Oui mais moi c'est ça qui m'a faire rire!
Re: un regard sur la conjecture de Collatz
Pour ceux que ça intéresse, l'algorithme "3n+1" s'inscrit dans un algorithme plus large :
Soit le couple d'entiers naturels (a, a-1).
Pour Un = b : si b divisible par (a-1) alors U(n+1) = b/(a-1), sinon U(n+1)= [a*b/(a-1)] + 1 .
Pour les couples (3,2) et (6,5) : 1 seule boucle identifiée (qui passe par 1)
Pour les couples (4,3) (5,4) : 2 boucles identifiées.
Pour le couple (7,6) : 3 boucles identifiées.
......
Les boucles identifiées se repèrent assez vite avec les petits nombres ( de l'ordre des centaines)
Il existe toujours une boucle qui repasse par 1 (ce qui est normal vu que (a-1)² = 1 [a] )
Toute suite tombe dans l'une des boucles identifiées.
Bien entendu, il ne s'agit ici que de constats sur des nombres jusqu'à au plus quelques centaines et ne préjuge rien sur des tests pouvant être réalisés sur des nombres plus grands (sauf que par sondage on n'en trouve pas d'autres)
Soit le couple d'entiers naturels (a, a-1).
Pour Un = b : si b divisible par (a-1) alors U(n+1) = b/(a-1), sinon U(n+1)= [a*b/(a-1)] + 1 .
Pour les couples (3,2) et (6,5) : 1 seule boucle identifiée (qui passe par 1)
Pour les couples (4,3) (5,4) : 2 boucles identifiées.
Pour le couple (7,6) : 3 boucles identifiées.
......
Les boucles identifiées se repèrent assez vite avec les petits nombres ( de l'ordre des centaines)
Il existe toujours une boucle qui repasse par 1 (ce qui est normal vu que (a-1)² = 1 [a] )
Toute suite tombe dans l'une des boucles identifiées.
Bien entendu, il ne s'agit ici que de constats sur des nombres jusqu'à au plus quelques centaines et ne préjuge rien sur des tests pouvant être réalisés sur des nombres plus grands (sauf que par sondage on n'en trouve pas d'autres)
Re: un regard sur la conjecture de Collatz
Bonsoir,
Pour ma part, je me suis intéressée pour la 1ère fois à cette conjecture (suite aux messages de @CAMI).
Voici mes conclusions (fait avec un tableau Excel), pour ceux que cela intéresse :
Les nombres pairs s'arrêtent en 1 pas (évident).
Les 4n+1 s'arrêtent en 3 pas. Restent les 4n+3.
Les 16n+3 s'arrêtent en 6 pas, les 32n+11 et les 32n+23 en 8 pas.
Restent les 32n+7, 15, 27, 31.
Les 128n+7, 15, 59 s'arrêtent en 11 pas, les 256n+39, 175, 219, 95 s'arrêtent en 13 pas.
Reste quelques régularités (très peu). Mais la majorité du reste (donc moins d'1/8 des nombres) n'a pas de règle établie apparente. Certains disparates (parmi les 150000 premiers) atteignent plus de 200 pas. Certains s'arrêtent en 19, 26 pas .... (certains nombres de pas reviennent, d'autres jamais). Certains au début font près de 100 pas. C'est très erratique pour les restants. Mais en moyenne le nombre de pas n'augmente pas avec le nombre de départ de la suite.
Rien n'explique que des nombres comme 113383 s'arrêtent en plus de 218 pas (elle fait constamment du pair, impair).
Donc c'est effectivement diabolique. Je m'arrêterai là, je pense que c'est une grosse perte de temps.
Petite précision : j'ai compté le nombre de pas jusqu'à ce que le nombre atteint pour la suite passe en-dessous du nombre de départ (car s'il atteint un nombre en-dessous de lui, il redescend jusqu'à 1).
Sinon, la suite 3n-1 a au moins 3 boucles, qui se finissent par 1, 7 et 61. La suite 5n+1 s'envole.
Pour ma part, je me suis intéressée pour la 1ère fois à cette conjecture (suite aux messages de @CAMI).
Voici mes conclusions (fait avec un tableau Excel), pour ceux que cela intéresse :
Les nombres pairs s'arrêtent en 1 pas (évident).
Les 4n+1 s'arrêtent en 3 pas. Restent les 4n+3.
Les 16n+3 s'arrêtent en 6 pas, les 32n+11 et les 32n+23 en 8 pas.
Restent les 32n+7, 15, 27, 31.
Les 128n+7, 15, 59 s'arrêtent en 11 pas, les 256n+39, 175, 219, 95 s'arrêtent en 13 pas.
Reste quelques régularités (très peu). Mais la majorité du reste (donc moins d'1/8 des nombres) n'a pas de règle établie apparente. Certains disparates (parmi les 150000 premiers) atteignent plus de 200 pas. Certains s'arrêtent en 19, 26 pas .... (certains nombres de pas reviennent, d'autres jamais). Certains au début font près de 100 pas. C'est très erratique pour les restants. Mais en moyenne le nombre de pas n'augmente pas avec le nombre de départ de la suite.
Rien n'explique que des nombres comme 113383 s'arrêtent en plus de 218 pas (elle fait constamment du pair, impair).
Donc c'est effectivement diabolique. Je m'arrêterai là, je pense que c'est une grosse perte de temps.
Petite précision : j'ai compté le nombre de pas jusqu'à ce que le nombre atteint pour la suite passe en-dessous du nombre de départ (car s'il atteint un nombre en-dessous de lui, il redescend jusqu'à 1).
Sinon, la suite 3n-1 a au moins 3 boucles, qui se finissent par 1, 7 et 61. La suite 5n+1 s'envole.
Modifié en dernier par Pseuda le 16 Aoû 2018, 22:24, modifié 2 fois.
Re: un regard sur la conjecture de Collatz
Bonjour
@pseuda Il y des trucs que je ne comprends pas:
par exemple tu dis que "les 4n+1 s'arrêtent en 3 pas"?
par exemple 41=4*10+1, la suite de 41 est finie est vaut:
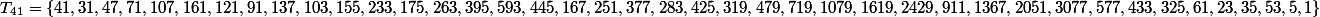
Inversement 41 a une infinité d'antécédents (impairs). Là je ne comprends pas.
Remarque: Pour certains la suite de Collatz d'un nombre m, notée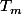
est constitué uniquement des nombres pairs. Le poids h(m) correspond alors au nombre d'éléments de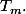
Ici h(41)=41. (coïncidence)
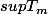 =le + grand élément s'il existe
=le + grand élément s'il existe
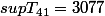
Un résultat connu quand m augmente) n'est pas borné.
n'est pas borné.
@pseuda Il y des trucs que je ne comprends pas:
par exemple tu dis que "les 4n+1 s'arrêtent en 3 pas"?
par exemple 41=4*10+1, la suite de 41 est finie est vaut:
Inversement 41 a une infinité d'antécédents (impairs). Là je ne comprends pas.
Remarque: Pour certains la suite de Collatz d'un nombre m, notée
est constitué uniquement des nombres pairs. Le poids h(m) correspond alors au nombre d'éléments de
Ici h(41)=41. (coïncidence)
Un résultat connu quand m augmente
Modifié en dernier par aviateur le 16 Aoû 2018, 21:38, modifié 1 fois.
Re: un regard sur la conjecture de Collatz
Bonjour @pseuda , j'ai pas compris le quart de la moitié de votre écrit, j'en suis réduit à faire des hypothèses, je vous cite: "les nombres pairs s'arrêtent en 1 pas (évident)", voudrai dire que tout nombre pair de la forme (4^n-1)*2^k/3 a pour successeur impair unique 1?
Quand à la suite il faudra être plus précise si vous voulez être comprise.
Je tient à votre disposition et à toute autre personne intéressée un fichier EXCEL qui contient la clef de la conjecture, il suffit de me faire savoir à quelle adresse mail vous l'envoyer.
Quand à la suite il faudra être plus précise si vous voulez être comprise.
Je tient à votre disposition et à toute autre personne intéressée un fichier EXCEL qui contient la clef de la conjecture, il suffit de me faire savoir à quelle adresse mail vous l'envoyer.
Re: un regard sur la conjecture de Collatz
Rebonjour
Encore un truc intéressant sur la conjecture.
On note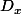 l'ensemble des nombres naturels impairs inférieurs ou égaux à x.
l'ensemble des nombres naturels impairs inférieurs ou égaux à x.
On note=2/x \sum_{m\leq x} h(m)) c'est à dire que cela représente une sorte de moyenne
c'est à dire que cela représente une sorte de moyenne
des longueurs suites.
Alors quand x tend vers l'infini on a\sim 2/log(16/9) log(x).)
En fait ce n'est pas démontré mais c'est une conjecture.
Par exemple pour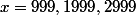 on trouve
on trouve / 2/log(16/9) log(x))
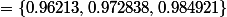
Que cette conjecture soit vraie ou fausse, ce qui est remarquable c'est déjà de trouver cela.
A propos des cycles il n'y a pas de 1-cycles (autre que 1) et il n'y a pas de 2-cycles (cela se démontre)
Concernant des cycles plus grand je ne sais pas s'il y a des résultats.
C'est surement un problème passionnant qui pose beaucoup plus de questions que de réponses.
Encore un truc intéressant sur la conjecture.
On note
On note
des longueurs suites.
Alors quand x tend vers l'infini on a
En fait ce n'est pas démontré mais c'est une conjecture.
Par exemple pour
Que cette conjecture soit vraie ou fausse, ce qui est remarquable c'est déjà de trouver cela.
A propos des cycles il n'y a pas de 1-cycles (autre que 1) et il n'y a pas de 2-cycles (cela se démontre)
Concernant des cycles plus grand je ne sais pas s'il y a des résultats.
C'est surement un problème passionnant qui pose beaucoup plus de questions que de réponses.
Re: un regard sur la conjecture de Collatz
aviateur a écrit:Bonjour
@pseuda Il y des trucs que je ne comprends pas:
par exemple tu dis que "les 4n+1 s'arrêtent en 3 pas"?
par exemple 41=4*10+1, la suite de 41 est finie est vaut:.
La suite démarrant à 41 s'arrête en 3 pas : 41 - 124 - 62 - 31 < 41
C'est pourquoi j'ai mis en gras la petite précision, à savoir qu'on s'arrête quand on atteint un nombre inférieur au 1er terme de la suite.
En effet, on n'a pas besoin de continuer car on est déjà passé par 31 et on sait qu'on est revenu à 1 avec 31.
Modifié en dernier par Pseuda le 16 Aoû 2018, 21:46, modifié 1 fois.
76 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
