Proprietes de congruence

[leon1789]

m² est un multiple de a²b² et donc m est un multiple de ab.

c'est faux !

[juve1897]

peux tu m'expliquer pourquoi est ce que c'est faux s'il te plait ?

[leon1789]

peux tu m'expliquer pourquoi est ce que c'est faux s'il te plait ?

ben, heu, l'explication ? ...la précipitation de ma réponse ! :triste:
(J'ai confondu avec autre chose.)
Ce que dit Doraki correspond à la seconde technique que je t'ai signalée :id:

[juve1897]

J'ai une proposition de solution :

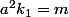
Si = m, alors il existe k_1,k_2 tels que et
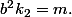
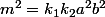
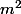
Donc donc ets un multiple de
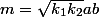
Ainsi et donc m est un multiple de ab.
donc = =
car on sait que



Je pense avoir à peu près le truc, mais je trouve que la rédaction c'est pas encore ça.

[leon1789]

Ainsi m = sqrt(k1k2)*ab et donc m est un multiple de ab.

Pour le coup, c'est pas tout à fait satisfaisant cette fois...

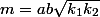
dans , la racine carrée est-elle un entier pour assurer que m est multiple de ab ?

[leon1789]

ppcm(a^2,ab,b^2) = ppcm(a^2,b^2,ab) = k1*k2

je croyais que c'était m le ppcm !?

[leon1789]

= =
car on sait que

:hein: je ne pense pas... !

[Doraki]

J'ai une proposition de solution :

Si ppcm(a^2;b^2) = m, alors il existe k1,k2 tels que a^2*k1 = m et b^2*k2 = m.
Donc m^2 = k1k2*a^2*b^2 donc m^2 ets un multiple de a^2*b^2.
Ainsi m = sqrt(k1k2)*ab et donc m est un multiple de ab.

ok, tu peux dire que k1k2 est un carré k² parceque c'est m²/a²b², et ensuite avoir m= kab,
c'est plus joli quand t'as pas des racines qui trainent qui font croire que t'as des trucs pas entiers.

donc ppcm(a^2,ab,b^2) = ppcm(a^2,b^2,ab) = k1*k2 car on sait que
k1*a^2 = m
k2*b^2 = m
sqrt(k1k2)ab = m.

ppcm(a²,b²) t'as dit que c'était m, à mon avis c'est resté m.

arf, ninja'd

[juve1897]

Ben comment faire alors, je vois pas trop là.

[leon1789]

ok, tu peux dire que k1k2 est un carré k² parceque c'est m²/a²b²
c'est plus joli quand t'as pas des racines qui trainent qui font croire que t'as des trucs pas entiers.

oui, mais là, k²=m²/a²b² c'est une fraction. Il faut justifier que k un entier...

[Doraki]

bah sachant que k1k2 est un entier et que c'est aussi le carré d'un rationnel, j'pense pas que ce soit osé de déduire que k1k2 est le carré d'un entier.

[juve1897]

Ok donc .
A présent la solution est-elle juste?

[leon1789]

bah sachant que k1k2 est un entier et que c'est aussi le carré d'un rationnel, j'pense pas que ce soit osé de déduire que k1k2 est le carré d'un entier.

oui et non, tout dépend du niveau de la personne qui rédige, et comment c'est rédigé : avec une petite phrase soulignant le fait, c'est mieux que de passer sous silence.

[leon1789]

Ok donc .
A présent la solution est-elle juste?

Le problème n'est pas de proouver : ça, on l'a depuis leur définition. Mais de prouver .

Soit on le prouve, soit on signale clairement la propriété ad hoc. Mais on ne passe pas sous silence le truc... (ou comme si on n'avait pas vu le problème... :we: )

[juve1897]

Ben je ne vois pas comment le prouver.

Pouvez vous me proposer un element de reponse/

[leon1789]

ok. Je reprends le début :

J'ai une proposition de solution :

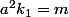
Si = m, alors il existe k_1,k_2 tels que et
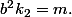
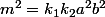
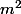
Donc donc ets un multiple de
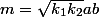
Ainsi (si )

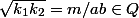
(:!: si a,b non nuls...)
Or il y a une proposition qui dit que
>
(--> faut-il encore connaitre cette proposition et sa démonstration...)

Donc

donc m est un multiple de ab.
donc ...

Par tout mon baratin, je voulais dire qu'il faut justifier correctement toutes les lignes, sans aller trop vite, sinon c'est pas satisfaisant.

[juve1897]

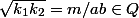
(:!: si a,b non nuls...)
Or il y a une proposition qui dit que
>
(--> faut-il encore connaître cette proposition et sa démonstration...)

Je connais la démonstration de \sqrt{2} n'est pas rationnel je pense que le principe est le même.

Donc pour résumer:


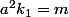
et

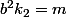
Donc on a

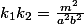
Etant donné que la racine carré de est rationnelle, il vient que cette racine est entiere.

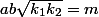
D'où (avec )

donc

CQFD

Est ce que c'est bon comme ça ???

[juve1897]

QQun peut me repondre SVP.

[leon1789]

Je connais la démonstration de \sqrt{2} n'est pas rationnel je pense que le principe est le même.

Par exemple, voir ce petit post
http://maths-forum.com/showthread.php?p=426010#post426010

=> et

Donc on a donc (si )

Etant donné que la racine carré de est rationnelle, il vient que cette racine est entiere.

D'où avec

donc m est multiple de ab

Cela montre que l'ensemble des multiples commun de a²,b² est inclus dans l'ensemble des multiples communs de a²,b² et ab.

Comme l'inclusion réciproque est évidente, on conclut



CQFD

ok, c'est bon comme ça pour moi.



question : a-t-on réellement utilisé que m = ppcm(a²,b²) ?
La réponse est non : on a juste utilisé que m est un multiple commun à a² et b²...

[juve1897]

question : a-t-on réellement utilisé que m = ppcm(a²,b²) ?
La réponse est non : on a juste utilisé que m est un multiple commun à a² et b²...

Ben en quelque sorte. Nous nous sommes servi de pour trouver le multiple commun.


Merci pour ta correction