Proprietes de congruence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:44
par juve1897 » 28 Aoû 2008, 19:44
leon1789 a écrit:Je te fais voir pour
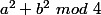
et tu le feras pour
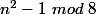
Maintenant on considère

impair : à quoi peut-il être congru modulo 8 ?
n peut etre congrue a
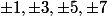
donc
pour n =
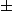
1 + 8k

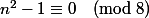
pour n=
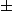
3 +8k

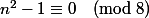
Donc 8 divise bien n^2 -1
C'est ça ???

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 28 Aoû 2008, 19:47
par raito123 » 28 Aoû 2008, 19:47
juve1897 a écrit:n peut etre congrue a
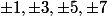
:doh:
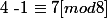
...
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:48
par leon1789 » 28 Aoû 2008, 19:48
juve1897 a écrit:n peut etre congrue a
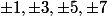
oui, et
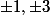
suffira , car 5=-3 et 7=-1 modulo 8 :id:
modulo 8, on a
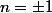
ou
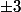
modulo 8, on a

= ... ?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:49
par juve1897 » 28 Aoû 2008, 19:49
raito123 a écrit::doh:
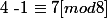
...
Je le sais je ne suis pas bête.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:50
par juve1897 » 28 Aoû 2008, 19:50
leon1789 a écrit:oui, et
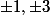
suffira , car 5=-3 et 7=-1 modulo 8 :id:
modulo 8, on a
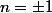
ou
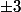
modulo 8, on a

= ... ?
Peux tu aller voir plus haut mon post, j'ai réedité en developpant ma demo

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 28 Aoû 2008, 19:51
par raito123 » 28 Aoû 2008, 19:51
donc il suffisait de dire que n est congru à 1 , 3 , 5 , 7 mod 8 , non ?
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:55
par leon1789 » 28 Aoû 2008, 19:55
Je corrige.
C'est ok, mais soit plus légère dans les écritures. Par exemple, comme ça :
n peut etre congru a
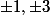
modulo 8
donc
modulo 8, pour n =
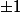
, on a

pour n=
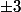
, on a

Donc
dans Z, 8 divise bien
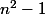
Tu vois que c'est plus reposant que ton raisonnement par récurrence, non ? :id:
Cela dit, il faut bien faire attention et bien dissocier ce qui se passe dans Z, et modulo 8.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:55
par leon1789 » 28 Aoû 2008, 19:55
raito123 a écrit:donc il suffisait de dire que n est congru à 1 , 3 , 5 , 7 mod 8 , non ?
oui c'est vrai. On peut aussi dire
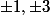
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:56
par juve1897 » 28 Aoû 2008, 19:56
leon1789 a écrit:Je corrige.
C'est ok, mais soit plus légère dans les écritures. Par exemple, comme ça :
Tu vois que c'est plus reposant que ton raisonnement par récurrence, non ? :id:
Oui tu as tout à fait raison.
Je n'y aurais jamais pensé.
donc tu penses que tout problème de divisibilité peut se resoudre par cette methode.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 28 Aoû 2008, 19:57
par raito123 » 28 Aoû 2008, 19:57
juve1897 a écrit:
donc tu penses que tout problème de divisibilité peut se resoudre par cette methode.
Moi je dis : pas forcément !!
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:03
par leon1789 » 28 Aoû 2008, 20:03
C'est quelque chose de très important le calcul modulaire !
juve1897 a écrit:donc tu penses que tout problème de divisibilité peut se resoudre par cette methode.
oula, je ne connais pas tous les problèmes de divisibilité ... :we: pas tous, comme dit ratio123
mais prends un autre exo (à coté de ceux que tu as fais ici) et je suis prêt à parier que tu peux le faire ainsi.
Par exemple :
montrer que 6 divise
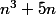
pour tout
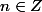
.
cf
http://maths-forum.com/showthread.php?p=427991#post427991
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:15
par juve1897 » 28 Aoû 2008, 20:15
leon1789 a écrit:C'est quelque chose de très important le calcul modulaire !
oula, je ne connais pas tous les problèmes de divisibilité ... :we: pas tous, comme dit ratio123
mais prends un autre exo (à coté de ceux que tu as fais ici) et je suis prêt à parier que tu peux le faire ainsi.
Par exemple :
montrer que 6 divise
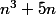
pour tout
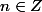
.
cf
http://maths-forum.com/showthread.php?p=427991#post427991
Ben je pense faire comme ça.
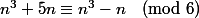
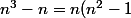 = n(n-1)(n+1))
Pour n=
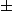
1
(n+1) = 0 + 6k)
Pour n=
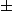
2
(n+1) = \pm2.1.3 = 0 + 6k)
Pour n= 3
(n+1) = 3.2.1 = 0 + 6k)
Donc on a bien 6 divise
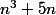
pour tout n

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 28 Aoû 2008, 20:23
par raito123 » 28 Aoû 2008, 20:23
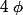
(6) = 2 !! (
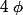
= indicatrice d'euler )
Donc
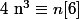
donc
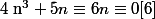
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:24
par leon1789 » 28 Aoû 2008, 20:24
juve1897 a écrit:Ben je pense faire comme ça.
(...)
Donc on a bien 6 divise
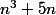
pour tout n
c'est ok ! :++:
Plus tard, tu verras que le calcul modulaire sert à plein d'autres choses que simplement vérifier des divisibilités un peu neuneu comme ça. :we:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:25
par juve1897 » 28 Aoû 2008, 20:25
raito123 a écrit: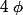
(6) = 2 !! (
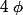
= indicatrice d'euler )
Donc
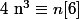
donc
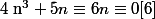
et ben dit donc toi, tu l'as fait en 1 ligne !

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:27
par leon1789 » 28 Aoû 2008, 20:27
raito123 a écrit: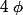
(6) = 2 !! (
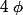
= indicatrice d'euler )
Donc
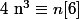
donc
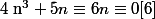
avec l'indicateur d'Euler, ok, mais encore une
chance que 6 est sans facteur carré pour avoir
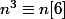
.
Dis-tu la même chose avec 9 ou 18 par exemple ? à savoir
+1} = n \ mod 9)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:28
par leon1789 » 28 Aoû 2008, 20:28
juve1897 a écrit:et ben dit donc toi, tu l'as fait en 1 ligne !
oui, mais il a fait un truc pas légal... :ptdr:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:29
par juve1897 » 28 Aoû 2008, 20:29
J'ai une autre affirmation que j'aimerai verifier:
Il y'a une infinité de couples d'entiers (x,y) tq
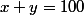
et
 = 5)
ben moi je commence par dire que pgcd(x,y)| 100
donc il y'a des solutions.
ensuite ???
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:30
par juve1897 » 28 Aoû 2008, 20:30
leon1789 a écrit:oui, mais il a fait un truc pas légal... :ptdr:
Ben mon prof, nous a dit d'utiliser l'indicatrice uniquement dans les cas où n (mod n) est premier.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:30
par leon1789 » 28 Aoû 2008, 20:30
juve1897 a écrit: = 5)
avec ça uniquement, que peux-tu dire de x et y ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
et tu le feras pour
impair : à quoi peut-il être congru modulo 8 ?
modulo 8
, on a
, on a
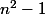
pour tout
.
pour tout
.