Polynôme..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Avr 2009, 07:46
par Dyo » 06 Avr 2009, 07:46
Bonjour !
J'ai un peu du mal à montrer qu'il existe un unique polynôme qui vérifie
=x^n+\frac{1}{x^n})
pour tout x réel non nul ...
Bon j'ai bien essayé de développer le truc et d'identifier les coeff, mais je trouve ça vraiment lourd et pas très intéressant. Y'a pas une autre méthode pour ce genre de problème ?
Merci

-
Ptiboudelard
- Membre Relatif
- Messages: 303
- Enregistré le: 31 Déc 2008, 08:43
-
 par Ptiboudelard » 06 Avr 2009, 07:52
par Ptiboudelard » 06 Avr 2009, 07:52
Bonjour ! Matinal à ce que je vois ? ;-)
Je suggère d'utiliser la méthode de la bijection ... Tu montre qu'il y a une solution unique et voilà !
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Avr 2009, 07:58
par Dyo » 06 Avr 2009, 07:58
J'avais pas encore réfléchi à l'unicité en fait ^^
Mais pour l'existence ? :p
-
mathelot
 par mathelot » 06 Avr 2009, 08:09
par mathelot » 06 Avr 2009, 08:09
Bj,
pour t'échauffer de bon matin, poser
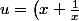)
et commence à écrire le développement de
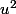
et
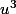
avec les identités remarquables...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 06 Avr 2009, 08:12
par leon1789 » 06 Avr 2009, 08:12
Dyo a écrit:Bonjour !
J'ai un peu du mal à montrer qu'il existe un unique polynôme qui vérifie
=x^n+\frac{1}{x^n})
pour tout x réel non nul ...
Bon j'ai bien essayé de développer le truc et d'identifier les coeff, mais je trouve ça vraiment lourd et pas très intéressant. Y'a pas une autre méthode pour ce genre de problème ?
Merci

Commence par le plus simple : l'unicité de Tn (j'imagine que tu travailles sur R...)
Ensuite, démontre l'existence de Tn (par exemple en suivant le conseil de mathelot)
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Avr 2009, 08:16
par Dyo » 06 Avr 2009, 08:16
Je travaille sur R en effet.
J'ai déjà fait ce que me suggère Mathelot, et au final ça revient à poser un système pour identifier les coefficients .. non ? Du moins c'est vers quoi j'aboutis.
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Avr 2009, 08:28
par Dyo » 06 Avr 2009, 08:28
J'avais obtenu deux équations :
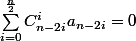
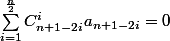
Mais bon je trouve ça un peu moche.
-
mathelot
 par mathelot » 06 Avr 2009, 08:44
par mathelot » 06 Avr 2009, 08:44
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 06 Avr 2009, 08:50
par Dyo » 06 Avr 2009, 08:50
ta méthode est critiquable (sauf le respect que je te dois )
En même temps si je poste sur le forum c'est pour qu'on me suggère des méthodes, et donc qu'on critique celles qui ne sont pas les bonnes :p
Ok donc je retrouve le u dans les développements, j'avais même pas fait attention à ça ^^
Merci bien !
-
mathelot
 par mathelot » 06 Avr 2009, 09:02
par mathelot » 06 Avr 2009, 09:02
re,
quand tu auras fini l'exo (uniquement quand tu l'auras fini avec la méthode demandée :we: ), il faudra jeter un oeil aux
polynômes de Tchebyshev.
Les siens

sont liés aux

de l'exercice par
=\frac{1}{2} T_n(2x))
-
mathelot
 par mathelot » 06 Avr 2009, 10:25
par mathelot » 06 Avr 2009, 10:25
re,
si on pose
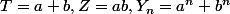
on aurait envie de réécrire les identités habituelles avec les nouvelles variables:
formule du binôme pour n=3
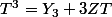
qui donnerait la pseudo-factorisation (on confond indice et exposant)
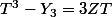
et aussi de regarder ce que donnent des pseudo-formules:
progression géométrique
}=P \sum_{k=0}^{\infty} \, (S-P)^k)
fonction formelle
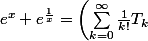 (x +\frac{1}{x}) =(e^T)(x +\frac{1}{x}))
etc..mais évidemment, si on trouve de jolies choses, ça ne surprendra pas les algébristes, et il faudra les démont(r)er sérieusement par la suite.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
