Polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MaxP06
- Messages: 3
- Enregistré le: 22 Mar 2019, 19:49
-
par MaxP06 » 22 Mar 2019, 20:08
Bonsoir, je rencontre des difficultés avec le problème suivant :
Déterminer les polynômes P tels que
^{2}|P-1)
et
^{2}|P+1)
J'ai essayé une première approche en essayant de trouver une relation avec les coefficients de P mais ça n'a rien donné. Puis j'ai essayé une autre approche en écrivant que :
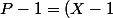^{2}Q)
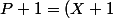^{2}R)
Avec Q et R des polynômes
J'ai travaillé ces expressions en les dérivant et regarder les valeurs en 1 et -1 mais je n'aboutis à rien de concret...
-
aviateur
par aviateur » 23 Mar 2019, 00:41
Bonjour
C'est l'ensemble des polynômes P de la forme
=\dfrac{3 X}{2}-\dfrac{X^3}{2}+(X^2-1)^2 R(X))
où
est un polynôme quelconque.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
par LB2 » 23 Mar 2019, 00:58
Tu peux dériver tes relations et en déduire une condition nécessaire sur P'(X)
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 23 Mar 2019, 15:29
Malgré les apparences , il s'agit essentiellement d'un problème linéaire :
^2)
divise
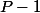
et
^2)
divise
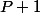
ssi
1 est racine double de
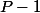
et - 1 est racine double de
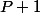
ssi
1 est racine de
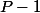
et 1 est racine de
')
et
- 1 est racine de
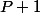
et 1 est racine de
')
ssi
=1)
et
=0)
et
=-1)
et
=0)
Soit f l'application de K[X] dans
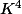
définie par
=(P(1),P'(1),P(-1),P'(-1)))
Il est facile de montrer que f est linéaire .
Donc l'ensemble cherché est l'ensemble des solutions de l'équation linéaire
=(1;0;-1;0))
Cet ensemble est donc de sructure connue : solution particulière + Ker(f)
Il te suffit de déterminer une solution particulière de degré 3 avec un solveur , Ker(f) étant évident .
-
MaxP06
- Messages: 3
- Enregistré le: 22 Mar 2019, 19:49
-
par MaxP06 » 23 Mar 2019, 17:03
Bonjour et merci à tous,
je n'ai pas encore vu les applications linéaires (c'est le chapitre que l'on attaque la semaine prochaine !) donc j'aimerais m'en sortir sans, j'ai donc suis vos conseils LB2 en dérivant mes expressions et en utilisant le fait que l'on peut procéder par identification avec la base (1, X, X²) et j'ai trouvé que Q'=R' et Q=-R ce qui me paraît louche car je n'aboutis pas à l'expression proposée par Aviateur.
-
aviateur
par aviateur » 23 Mar 2019, 19:20
Bonjour
Evidemment c'est un problème simple d'algèbre linéaire. Mais si tu ne l'a pas vu, tu peux faire la résolution uniquement à partir de la connaissance des polynômes en suivant une bonne logique :
Soit P et Q deux solutions:
divise donc P-1 et Q-1 donc divise la différence P-Q.
De même on montre que
divise P-Q.
Autrement dit
^2(X+1)^2=(X^2-1)^2)
divise P-Q
ou ce qui revient au même
-Q(X)=(X^2-1)^2R(X))
où R est un polynôme quelconque.
Il reste à chercher une solution. Pour cela on va chercher un polynôme de degré3
)
.
Des petit calculs vont donner celui que j'ai donné dans mon premier post.
d'où l'ensemble des solutions
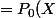+(X^2-1)^2R(X))
Modifié en dernier par aviateur le 23 Mar 2019, 21:48, modifié 1 fois.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 23 Mar 2019, 19:34
Merci aviateur . Et en plus la solution que tu proposes est plus simple .
-
aviateur
par aviateur » 23 Mar 2019, 21:50
@tournesol:
En fait j'avais fais comme tu as expliqué. i.e passer par P: R[X]--> (P(-1),P'(-1),P(1),P'(1)).
Mais bon avec moins de moyen on peut toujours s'en sortir aussi bien.
Ceci étant, dit vu qu'il va commencer à voir les applications linéaires c'est important qu'il voit qu'on a simplement une équation linéaire du type f(x)=y et que l'ensemble des solutions, s'il est non vide c'est
)
ou
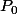
est une solution particulière.
-
MaxP06
- Messages: 3
- Enregistré le: 22 Mar 2019, 19:49
-
par MaxP06 » 24 Mar 2019, 10:37
Merci aviateur j'ai pu trouvé la solution en suivant vos conseils, j'essaierai en appliquant l'autre méthode quand j'aurai avancé dans le cours sur les applications linéaires.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
