Bonjour,
je n'arrive pas a faire cette demonstration:
Démontrer qu'un polynome caracteristique est de degré n.
Merci d'avance!
Polynome caracteristique
6 messages
- Page 1 sur 1
Re: polynome caracteristique
Salut.
Moi, j'arrive pas à montrer que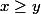 . Tu peut m'aider ?
. Tu peut m'aider ?
Plus sérieusement, tu pense vraiment que ta question, avec toute les magnifiques informations que tu nous donne concernant le contexte est qui représente quoi puisse avoir un sens ?
Par exemple, je te propose ça comme "preuve" :
Soit P un polynôme "caractéristique" (de quoi ?, on s'en fout, à coeff dans quel anneau/corps ? on s'en fout).
On pose) .
.
Et on a donc bien P qui est de degré n
Moi, j'arrive pas à montrer que
Plus sérieusement, tu pense vraiment que ta question, avec toute les magnifiques informations que tu nous donne concernant le contexte est qui représente quoi puisse avoir un sens ?
Par exemple, je te propose ça comme "preuve" :
Soit P un polynôme "caractéristique" (de quoi ?, on s'en fout, à coeff dans quel anneau/corps ? on s'en fout).
On pose
Et on a donc bien P qui est de degré n
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: polynome caracteristique
Bonjour;
d'abord, j'exprime ma solidarité et ma compassion à tous ceux qui ont été sinistrés par les intempéries qui touchent le Centre et l'Ile-de-France: comme francophone, ma boussole indique depuis toujours Paris, et mon cœur bat au rythme de LA MARSEILLAISE, et j'en suis fier.
Ceci dit, je crois que M.ben314 a raison d'insister sur l'importance de la définition du contexte, surtout que la démonstration demandée pour un polynôme caractéristique d'un endomorphisme en dimension finie est laborieuse.
d'abord, j'exprime ma solidarité et ma compassion à tous ceux qui ont été sinistrés par les intempéries qui touchent le Centre et l'Ile-de-France: comme francophone, ma boussole indique depuis toujours Paris, et mon cœur bat au rythme de LA MARSEILLAISE, et j'en suis fier.
Ceci dit, je crois que M.ben314 a raison d'insister sur l'importance de la définition du contexte, surtout que la démonstration demandée pour un polynôme caractéristique d'un endomorphisme en dimension finie est laborieuse.
Re: polynome caracteristique
Bonjour;
Le sujet du fil me paraît très intéressant, surtout que c'est une étape pour démontrer le théorème suivant:
Soit}) un
un  -espace vectoriel de dimension
-espace vectoriel de dimension 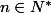 ,
,  un endomorphisme de E (je m'excuse, je n'ai pas su comment écrire le L(E)) , et
un endomorphisme de E (je m'excuse, je n'ai pas su comment écrire le L(E)) , et  le polynôme caractéristique de
le polynôme caractéristique de  ,
,
alors = \lambda^n - tr(u) \lambda^{n-1} + \ldots + (-1)^n \det(u)) avec
avec ) la trace de
la trace de  .
.
Soit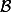 une base de \math E , et
une base de \math E , et  la matrice représentative de
la matrice représentative de  dans
dans  .
.
L'endomorphisme) de
de  a pour matrice représentative
a pour matrice représentative ) dans la base
dans la base 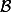 , donc
, donc  = \det(A - \lambda I_n)) .
.
Appelons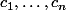 les vecteurs de
les vecteurs de  qui ont pour coordonnées dans la base canonique
qui ont pour coordonnées dans la base canonique 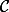 de
de les valeurs apparaissant en colonnes dans
les valeurs apparaissant en colonnes dans  , et
, et  les vecteurs de
les vecteurs de 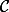 ,
,
alors = \det_{\mathcal{C}}(c_1-\lambda e_1,\ldots,c_n-\lambda e_n)) et
et 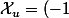^n \det_{\mathcal{C}}(c_1-\lambda e_1,\ldots,c_n-\lambda e_n)) .
.
On peut donc développer ce déterminant par n-linéarité et obtenir termes en tout , et affirmer que
termes en tout , et affirmer que  est une expression polynômiale en \lambda à coefficients dans K .
est une expression polynômiale en \lambda à coefficients dans K .
Le terme de plus haut degré correspond à l'unique terme où n'apparaissent que les) , donc c'est le terme
, donc c'est le terme ^n \det(- \lambda e_1,\ldots,-\lambda e_n) = (-1)^n (-1)^n \lambda^n\det(e_1,\ldots,e_n) = \lambda^n\det(e_1,\ldots,e_n) = \lambda^n) , donc
, donc  est de degré n.
est de degré n.
Le terme constant correspond lui aussi à l'unique terme où n'apparaissent que les , donc c'est le terme
, donc c'est le terme ^n \det(c_1,\ldots,c_n) = (-1)^n \det(A) = (-1)^n\det(u)) .
.
Pour le terme de degré (n-1) je laisserai la démonstration pour autrui.
Cette démonstration - pour être franc - n'est pas de mon œuvre, c'est une des que nous avons fait au cours et donc beaucoup de versions se trouvent sur le Net.
Merci.
Le sujet du fil me paraît très intéressant, surtout que c'est une étape pour démontrer le théorème suivant:
Soit
alors
Soit
L'endomorphisme
Appelons
alors
On peut donc développer ce déterminant par n-linéarité et obtenir
Le terme de plus haut degré correspond à l'unique terme où n'apparaissent que les
Le terme constant correspond lui aussi à l'unique terme où n'apparaissent que les
Pour le terme de degré (n-1) je laisserai la démonstration pour autrui.
Cette démonstration - pour être franc - n'est pas de mon œuvre, c'est une des que nous avons fait au cours et donc beaucoup de versions se trouvent sur le Net.
Merci.
Re: polynome caracteristique
Bonjour,
Une autre façon de voir les choses serait de revenir à la définition du déterminant par la formule de Leibniz, qui s'écrit pour _{1\leq i,j\leq n}) :
:
=\displaystyle\sum_{\sigma\in\mathfrak{S}_n}\varepsilon (\sigma)\displaystyle\prod_{i=1}^n a_{\sigma (i),i}) .
.
Elle semble barbare a priori, mais en fait, tout ce qu'elle veut dire, c'est que le déterminant d'une matrice est la somme sur tous les choix de coefficients possibles de telle sorte qu'on en prenne exactement un par colonne et par ligne. Cette définition donne alors
=\prod(\lambda -u_{i,i}) + \cdots = \lambda ^n-\mathrm{tr}(u)\lambda ^{n-1} + \cdots) .
.
On montre par cette même formule qu'il n'y a pas d'autres termes d'ordre (càd si on "choisit"
(càd si on "choisit"  coefficients sur la diagonale dans le calcul du déterminant, alors la formule de Leibniz nous dit que le dernier coefficient est aussi sur la diagonale. Autre formulation équivalente : il n'existe pas de permutation de
coefficients sur la diagonale dans le calcul du déterminant, alors la formule de Leibniz nous dit que le dernier coefficient est aussi sur la diagonale. Autre formulation équivalente : il n'existe pas de permutation de ) qui possède exactement
qui possède exactement  points fixes).
points fixes).
Enfin, on trouve le dernier coefficient en calculant) , ce qui donne
, ce qui donne ^n\det (u)) .
.
Au passage, tu peux utiliser \mathcal{L}(E) pour avoir) (certains n'aiment pas, mais bon)
(certains n'aiment pas, mais bon) 
Une autre façon de voir les choses serait de revenir à la définition du déterminant par la formule de Leibniz, qui s'écrit pour
Elle semble barbare a priori, mais en fait, tout ce qu'elle veut dire, c'est que le déterminant d'une matrice est la somme sur tous les choix de coefficients possibles de telle sorte qu'on en prenne exactement un par colonne et par ligne. Cette définition donne alors
On montre par cette même formule qu'il n'y a pas d'autres termes d'ordre
Enfin, on trouve le dernier coefficient en calculant
Au passage, tu peux utiliser \mathcal{L}(E) pour avoir
Re: polynome caracteristique
Merci pour l'intérêt que vous avez porté à ma démonstration, ainsi que pour le tuyau "Latex" .
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
