[Topologie] point d'accumulation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 06 Jan 2007, 13:46
par Epsilon » 06 Jan 2007, 13:46
Aidez moi svp :triste: :triste:
bonjour
dans la topologie usuelle de IR (IR,| |).
Soit A={ 1/(n+1), nIN }
-Monter que 0 est un point d'accumulation de l'ensemble A.
merci d'avance.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 13:52
par tize » 06 Jan 2007, 13:52
C'est pas très dur, écris la définition d'un point d'accumulation d'abord...
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 06 Jan 2007, 13:56
par Epsilon » 06 Jan 2007, 13:56
la défi:
x est un pt d'accumulation de A ssi
qqsoit v V(x) : (v-{x}) inter A <> de l'ens vide
mais je vois pas comment je commence
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 14:02
par tize » 06 Jan 2007, 14:02
Bien il revient au même de montrer que pour tout
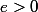
,
\cap A \neq \emptyset)
]-e;e[ étant le voisinage de 0...
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 06 Jan 2007, 14:08
par Epsilon » 06 Jan 2007, 14:08
on ne peut pas utiliser raisonnemnt par l'absurde !
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 14:09
par tize » 06 Jan 2007, 14:09
Oui on peut...supposons que 0 n'est pas un point d'accumulation alors : négation de la définition...
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 06 Jan 2007, 14:14
par Epsilon » 06 Jan 2007, 14:14
je me bloque aussi
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 14:39
par tize » 06 Jan 2007, 14:39
Ba la négation de :
,\;\(V-\{0\}\)\cap A\neq\emptyset)
est :
,\;\(V-\{0\}\)\cap A=\emptyset)
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 06 Jan 2007, 14:51
par cesar » 06 Jan 2007, 14:51
pourquoi se casser la tete ??
prenez un voisinage de 0 quelconque, mais fixé et comme la suite 1/(n+1) tend vers 0 lorsque n tend vers l'infini, vous trouvez que pour n assez grand, 1/(n+1) sera dans le voisinage...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 14:54
par tize » 06 Jan 2007, 14:54
cesar a écrit:pourquoi se casser la tete ??
prenez un voisinage de 0 quelconque, mais fixé et comme la suite 1/(n+1) tend vers 0 lorsque n tend vers l'infini, vous trouvez que pour n assez grand, 1/(n+1) sera dans le voisinage...
Merci Cesar :triste: mais le but ici n'était pas de donner la réponse à Epsilon mais de l'amener à trouver tout seul...
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 06 Jan 2007, 15:23
par Epsilon » 06 Jan 2007, 15:23
merci cesar et grand grand merci à tize
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
