Point d'accumulation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
freestyle58
- Membre Relatif
- Messages: 279
- Enregistré le: 02 Juil 2007, 03:42
-
 par freestyle58 » 23 Sep 2010, 21:39
par freestyle58 » 23 Sep 2010, 21:39
Bonjour,
Voici mon problème:
Soit E un ensemble arbitraire de nombres réels. Montrer que E' est fermé (E' étant l'ensemble des points d'accumulation de E).
J'ignore complètement comment débuter ma preuve. Pouvez-vous m'aider ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Sep 2010, 21:47
par girdav » 23 Sep 2010, 21:47
Bonjour,
peux-tu commencer par donner la définition de points d'accumulation? (je sais ce que c'est ne t'inquiète pas, c'est juste qu'il est toujours bon de se rappeler les définitions avant de débuter un exercice)
-
freestyle58
- Membre Relatif
- Messages: 279
- Enregistré le: 02 Juil 2007, 03:42
-
 par freestyle58 » 23 Sep 2010, 21:57
par freestyle58 » 23 Sep 2010, 21:57
ma définition de point d'accumulation est la suivante:
Un point a est un point d'accumulation d'un ensemble E si tout voisinage de a contient un point de E autre que a.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Sep 2010, 21:59
par girdav » 23 Sep 2010, 21:59
D'accord.
On peut essayer de montrer que le complémentaire de
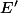
est un ouvert. Pour cela, si

n'est pas un point d'accumulation de

alors on peut trouver un intervalle ouvert centré en

qui ne rencontre pas

. Il te reste à montrer que cet intervalle ne contient pas de points d'accumulation de

.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Sep 2010, 23:18
par Nightmare » 23 Sep 2010, 23:18
Salut,
autre approche : les seuls éléments qu'il manque pour être dans la fermeture de E, ce sont les éléments isolés ...
-
freestyle58
- Membre Relatif
- Messages: 279
- Enregistré le: 02 Juil 2007, 03:42
-
 par freestyle58 » 24 Sep 2010, 01:26
par freestyle58 » 24 Sep 2010, 01:26
tu entends quoi par éléments isolés?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Sep 2010, 10:00
par girdav » 24 Sep 2010, 10:00
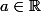
(*) est dit isolé pour

s'il existe un voisinage de

privé de

(**) est disjoint de

. Par exemple, avec
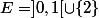
on montre que

est un point isolé pour

.
edit : (*),(**) coquilles de ma part.
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 24 Sep 2010, 10:22
par Arkhnor » 24 Sep 2010, 10:22
Bonjour.
Si

appartient à

, un voisinage de

a peu de chances d'être disjoint de

...
Un point isolé de E, c'est un point
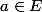
tel que
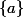
est ouvert dans E pour la topologie induite.
En d'autres termes, il existe un voisinage de

disjoint de
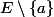
.
-
mathelot
 par mathelot » 24 Sep 2010, 12:27
par mathelot » 24 Sep 2010, 12:27
Bonjour,
soit L une limite de points de E'
Tout voisinage ouvert de L contient un point e'. Comme il est ouvert
c'est un voisinage de e'. Il contient donc un point e de E dans une boule
ouverte de centre e' et de rayon r < d(e',L). donc
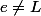
-
freestyle58
- Membre Relatif
- Messages: 279
- Enregistré le: 02 Juil 2007, 03:42
-
 par freestyle58 » 24 Sep 2010, 18:14
par freestyle58 » 24 Sep 2010, 18:14
Comment fait-on pour montrer que cet intervalle ne contient pas de points d'accumulation de E ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Sep 2010, 18:53
par girdav » 24 Sep 2010, 18:53
Prends un point

dans cet intervalle

. Il existe un
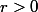
tel que l'intervalle
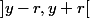
soit entièrement contenu dans

.
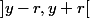
ne peut pas rencontrer

et ça marche car

est arbitraire.
-
freestyle58
- Membre Relatif
- Messages: 279
- Enregistré le: 02 Juil 2007, 03:42
-
 par freestyle58 » 25 Sep 2010, 00:28
par freestyle58 » 25 Sep 2010, 00:28
merci pour votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
