Point d'accumulation

[momokani]

Bonjours,

Comment peut-on prouver que si ,
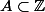
n'a pas de point d'accumulation?

Merci

[L.A.]

Bonjour.

Z étant discret, tout singleton est ouvert et donc un point x ne peut pas être limite d'une suite de points de Z privé de {x} qui est fermé.

[momokani]

Peux-tu expliquer un peu plus, je pense pas que je comprends ce que tu veux dire.

[eratos]

salut!

Peux-tu expliquer un peu plus, je pense pas que je comprends ce que tu veux dire.

Z/{x} est fermé donc égale à son adhérence, comme les suites de Z/{x} qui convergent le font dans Z/{x} ,les limites de telles suites sont différentes de x. x n'est donc pas un point d'accumulation

[arnaud32]

Bonjours,

Comment peut-on prouver que si ,
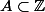
n'a pas de point d'accumulation?

Merci

c'est quoi pour toi un point d'accumulation?

[momokani]

Dans un continuum, un point d'accumulation d'une partie A est un point x de l'adhérence de A\{x}, c'est-à-dire tel que tout ouvert contenant x contient au moins un autre point de A.

[mrif]

Dans un continuum, un point d'accumulation d'une partie A est un point x de l'adhérence de A\{x}, c'est-à-dire tel que tout ouvert contenant x contient au moins un autre point de A.

Soit a un élément de A. L'ouvert ]a-0.5 ; a+0.5[ ne contient aucun élément de Z (donc de A) autre que a, donc a n'est pas un point d'accumulation.

[eratos]

Soit a un élément de A. L'ouvert ]a-0.5 ; a+0.5[ ne contient aucun élément de Z (donc de A) autre que a, donc a n'est pas un point d'accumulation.

Je ne te suis pas, ton 'ouvert' n'est pas un ouvert dans Z. On a le droit de faire ça?

[mrif]

Je ne te suis pas, ton 'ouvert' n'est pas un ouvert dans Z. On a le droit de faire ça?

Si l'espace topologique est Z l'intervalle en question est ]a-0.5 ; a+0.5[ inter Z.

L'énoncé ne précise pas que l'espace topologique est Z. Si c'était le cas, la question n'aurait aucun intérêt puisque tout point de Z est un ouvert qui ne contient pas d'autre point.

Il est d'usage, en absence de précision, de considérer qu'il s'agit de l'espace topologique habituel: c'est à dire R muni de la distance euclidienne, et dans ce cas la question présente un petit intérêt.

[L.A.]

C'est la même chose non ? La topologie discrète sur Z est également la topologie induite par son plongement naturel dans R, R étant muni de sa topologie usuelle.

Autre façon de voir : montrer que toute suite convergente dans Z est en fait stationnaire.

[mrif]

C'est la même chose non ? La topologie discrète sur Z est également la topologie induite par son plongement naturel dans R, R étant muni de sa topologie usuelle.

Autre façon de voir : montrer que toute suite convergente dans Z est en fait stationnaire.

R et Z sont bien distincts en tant qu'espaces topologiques même si la topologie considérée sur Z est la topologie induite par celle de R: un ouvert de Z n'est pas necessairement un ouvert de R.