Norme opérateur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 04 Oct 2020, 11:59
par Davidmaths » 04 Oct 2020, 11:59
Bonjour,
J'ai un problème avec un exercice. Je réécris l'énoncé:
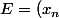_n \in R^n :)
il existe

pour tout

. On pose
_n \rightarrow (y_n)_n<br />\end{cases})
avec
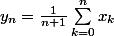
Vous calculerez la norme d'opérateur de

J'ai commencé par montrer que A est linéaire puis je veux montrer que A est aussi continue.
Mais pour montrer que A est continu j'ai un doute. Pouvons-nous dire que

est bornée car
_n)
appartient à

donc

est uniformément continue donc

continue ?
Ensuite, je n'ai aucune idée pour calculer la norme d'opérateur de T ...
Je remercie d'avance toutes les personnes qui vont m'apporter de l'aide et je vous souhaite une agréable journée !
Bien cordialement,
David
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Oct 2020, 13:09
par GaBuZoMeu » 04 Oct 2020, 13:09
Bonjour,
Quelques petites coquilles dans ta recopie d'énoncé.

est bien le sous espace de

(et pas

) formé des suites bornées ? Et tu as oublié de préciser la norme. Je suppose que
_n\Vert = \sup\{|x_n|\mid n \in \mathbb N\})
?
Ne peux-tu pas majorer
_n)\Vert)
en fonction de
_n\Vert)
?
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 04 Oct 2020, 13:38
par Davidmaths » 04 Oct 2020, 13:38
Bonjour GaBuZoMeu,
Oui effectivement je ne savais pas comment l'écrire en latex , c'est bien
GaBuZoMeu a écrit: le sous espace de

. E est donc l'espace vectoriel des suites réelles bonés muni de la norme sup (comme vous l'aviez suggéré)
En fait, quand on parle de norme d'opérateur il faut vérifier les 3 axiomes de la norme ? En effet je n'ai aucune définition dans mon cours avec le terme de "norme d'opérateur".
Cependant, si j'essaye de faire ce que vous dites,
je peux dire que :
_n)=(y_n)_n)
_n)||=||(y_n)_n||=sup \left\{ \frac{1}{n+1}\sum_{k=0}^{n}{x_k}, n\in \mathbb N \right\})
Or
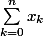
est borné car
_n \in E)
et
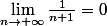
J'ai du mal à l'exprimer mais du coup je pense que
_n)|| \leq ||(x_n)_n||)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Oct 2020, 14:52
par GaBuZoMeu » 04 Oct 2020, 14:52
Une coquille dans ce que tu écris ( un

oublié).
Pour te dépatouller, pose
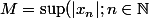 = \Vert (x_n)_n\Vert)
.
Peux-tu majorer

en fonction de

?
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 04 Oct 2020, 16:31
par Davidmaths » 04 Oct 2020, 16:31
Excusez-moi mais je ne vois pas où j'ai oublié
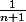
Donc
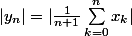
Donc il faut que je majore
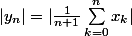
en fonction de
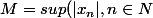
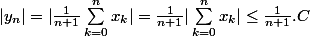
Et on a aussi que

Et je ne vois pas comment les regrouper
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Oct 2020, 16:48
par GaBuZoMeu » 04 Oct 2020, 16:48
Ici :
Davidmaths a écrit:Or
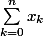
est borné car
_n \in E)
et
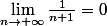
et par ailleurs ton argument ne va pas.
Ensuite : vraiment, si
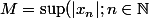)
, tu ne vois pas comment majorer
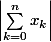
en faisant intervenir

??
Ça réparera aussi ton argument ci-dessus.
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 04 Oct 2020, 17:23
par Davidmaths » 04 Oct 2020, 17:23
J'ai peu être un idée,
on peut dire que

puis
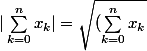^2} \leq \sqrt {\sum_{k=0}^{n}{M}} =M\sqrt{n+1})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Oct 2020, 22:44
par GaBuZoMeu » 04 Oct 2020, 22:44
Ça ne va pas.
Tout de même,, majorer
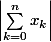
quand on a un majorant de tous les
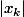
!!!
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 09:40
par Davidmaths » 05 Oct 2020, 09:40
On peut dire :
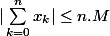
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 10:17
par GaBuZoMeu » 05 Oct 2020, 10:17
Compte mieux ! Ce n'est pas

.
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 10:41
par Davidmaths » 05 Oct 2020, 10:41
n+1 parce qu'on commence à 0
Si je reprends, on a dit que :
M)
donc
_n)||=||(y_n)_n|| \leq (n+1)M = (n+1) ||(x_n)_n||)
Donc comme vous me le demandiez au départ on arrive à :
_n)|| \leq (n+1) ||(x_n)_n||)
Je me suuis renseigné sur internet et j'ai vu que la norme d'opérateur (en utilisant les notations de cet exercice) :
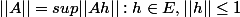
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 12:31
par GaBuZoMeu » 05 Oct 2020, 12:31
Davidmaths a écrit:Si je reprends, on a dit que :
M)
Non. Tu oublies encore une fois le

.
Sois un peu plus soigneux !
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 12:47
par Davidmaths » 05 Oct 2020, 12:47
Oui
on a dit excusez moi que:
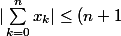M)
Donc
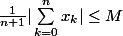
c'est à dire

Donc
_n)||= ||(y_n)_n|| \leq M = ||(x_n)_n||)
Donc
_n|| \leq ||(x_n)_n||)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 12:57
par GaBuZoMeu » 05 Oct 2020, 12:57
Bon. C'était un peu pénible, mais on y arrive.
Maintenant, que peux-tu déduire de la dernière inégalité concernant la norme de l'opérateur

?
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 13:10
par Davidmaths » 05 Oct 2020, 13:10
Oui je me suis un peu mélangé entre les valeurs absolues et normes pardonnez-moi
_n|| \leq sup{|x_n|, n\in N})
et
n_n||}{||x_n||})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 13:28
par GaBuZoMeu » 05 Oct 2020, 13:28
Ce que tu écris ne va pas, encore un manque de soin : fais bien la différence entre

et
la suite _n)
.
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 14:00
par Davidmaths » 05 Oct 2020, 14:00
Donc est-ce :
_n||}{||(x_n)_n||} \right\})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 14:09
par GaBuZoMeu » 05 Oct 2020, 14:09
Oui (en précisant tout de même que la suite
_n)
n'est pas nulle, et on peut se restreindre sans changement du résultat aux suites de norme 1).
Maintenant, peux-tu avancer dans ton problème ?
-
Davidmaths
- Membre Naturel
- Messages: 51
- Enregistré le: 05 Mai 2020, 18:02
-
 par Davidmaths » 05 Oct 2020, 14:15
par Davidmaths » 05 Oct 2020, 14:15
Oui je ne l'ai pas précisé mais c'est vrai et oui effectivement car toutes les normes sont équivalentes en dimension finie.
Justement je n'arrive pas à en déduire quelque chose avec l'inégalité
_n||\leq ||(x_n)_n||)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Oct 2020, 14:32
par GaBuZoMeu » 05 Oct 2020, 14:32
Essaie tout de même de voir plus loin que le bout de ton nez !
Tu as
_n)\Vert \leq \Vert(x_n)_n\Vert)
pour toute suite
_n)
et tu connais la définition
_n)\Vert}{\Vert(x_n)_n\Vert} ; (x_n)_n\neq 0\right))
.
Vraiment, tu ne vois rien à en déduire sur

???
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
