soit
Norme de l'inverse d'une application linéaire
10 messages
- Page 1 sur 1
Re: norme de l'inverse d'une application linéaire
Salut,
Ben prend un exemple (une bonne vieille matrice 2x2, éventuellement diagonale) et regarde si c'est vrai ou pas.
Ben prend un exemple (une bonne vieille matrice 2x2, éventuellement diagonale) et regarde si c'est vrai ou pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: norme de l'inverse d'une application linéaire
salut
non ce n'est pas vraie
puisque la dim est fini alors toutes les normes sont équivalente prenant la norme infini
alors si A = ( 5 0 0 6 ) alors , norme(A) = 6 et on a A-1 = ( 1/ 5 0 0 1/7 ) et donc norme(A-1) = 1/5
Par contre on a 1/norme(A-1 )<= norme(A)
Est-ce que ceci est vraie pour toujours ??
non ce n'est pas vraie
puisque la dim est fini alors toutes les normes sont équivalente prenant la norme infini
alors si A = ( 5 0 0 6 ) alors , norme(A) = 6 et on a A-1 = ( 1/ 5 0 0 1/7 ) et donc norme(A-1) = 1/5
Par contre on a 1/norme(A-1 )<= norme(A)
Est-ce que ceci est vraie pour toujours ??
Re: norme de l'inverse d'une application linéaire
Bonjour
Je n'ai rien compris à la manière dont tu écris des maths. Mais tu demandes si on a toujours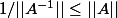 . Ne sais-tu pas que
. Ne sais-tu pas que ^{-1}=A) ?
?
Je n'ai rien compris à la manière dont tu écris des maths. Mais tu demandes si on a toujours
Re: norme de l'inverse d'une application linéaire
Relis ce que j'ai écrit dans mon premier post et réfléchis un peu!
Re: norme de l'inverse d'une application linéaire
Ça serait quand même pas con de revoir le B-A-BA des normes matricielles et plus précisément le notion de norme subordonnée :
L'ensemble des matrices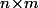 , c'est certes un espace vectoriel et jusque là, toute les normes "se valent" (et sont équivalentes vu qu'il est de dimension finie), mais c'est aussi, voire surtout, une représentation des applications linéaires de E=R^m dans F=R^m et, si E et F sont eux même des espaces vectoriels normés, alors ça induit naturellement une norme (dite subordonnée) sur l'e.v. L(E,F) des applications linéaires de E dans F via la définition on ne peut plus naturelle :
, c'est certes un espace vectoriel et jusque là, toute les normes "se valent" (et sont équivalentes vu qu'il est de dimension finie), mais c'est aussi, voire surtout, une représentation des applications linéaires de E=R^m dans F=R^m et, si E et F sont eux même des espaces vectoriels normés, alors ça induit naturellement une norme (dite subordonnée) sur l'e.v. L(E,F) des applications linéaires de E dans F via la définition on ne peut plus naturelle :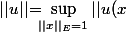||_F) pour tout
pour tout ) .
.
Et si on prend une telle norme (dite subordonnée) sur l'ensemble des endomorphisme, alors il est immédiat qu'on a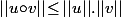 lorsque
lorsque 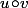 a du sens.
a du sens.
Et en particulier, si) alors
alors 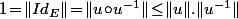 donc
donc 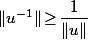 .
.
Et si ta norme n'est pas une norme subordonnée mais que tu est en dimension finie, alors elle est équivalente à une norme subordonnée et il existe donc forcément une constante K (dépendant de la norme et uniquement de la norme) telle que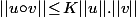 pour tout
pour tout ) et donc
et donc 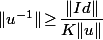 pour tout u dans
pour tout u dans )
L'ensemble des matrices
Et si on prend une telle norme (dite subordonnée) sur l'ensemble des endomorphisme, alors il est immédiat qu'on a
Et en particulier, si
Et si ta norme n'est pas une norme subordonnée mais que tu est en dimension finie, alors elle est équivalente à une norme subordonnée et il existe donc forcément une constante K (dépendant de la norme et uniquement de la norme) telle que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: norme de l'inverse d'une application linéaire
Et concernant ce type d'inégalité, même réponse que mon premier post : avant de poser ce type de question, ça te viendrait pas à l'esprit d'au moins regarder sur un exemple ce que ça donne ?klaimouad a écrit:mais est ce que cela est vraie
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
