Bonjour je dois montrer la continuité d'une application lineaire définie par :
u: AxB -> H
(x,y) -> x+y
H (Hilbert)
(A et B deux sous espace vectoriel de H tel que A inter B est réduit a 0)
J'ai une idée de comment faire en ayant la norme de u,
||u|| mais je n'ai aucun souvenir de comment on définie la norme d'une application lineaire (niveau L2 ou L3 pourtant) si quelqu'un pouvait me rafraichir la mémoire?
Merci d'avance!
Norme d'une application lineaire.
7 messages
- Page 1 sur 1
On peut définir la norme d'une application linéaire de plusieurs manière, l'une d'entre elles est :
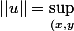\in A\times B,(x,y)\neq 0}\frac{|u(x,y)|}{|(x,y)|})
Si tu montres que le sup existe et est finie alors tu montres du même coup que u est continue car alors on a pour tout (x,y) :
|\leq ||u||\cdot|(x,y)|)
[edit]
J'ajouterai qu'ici ça n'est pas vraiment nécessaire, si on prend comme norme sur l'espace produit|=|x|+|y|) alors la continuité de u est immédiate...
alors la continuité de u est immédiate...
Si tu montres que le sup existe et est finie alors tu montres du même coup que u est continue car alors on a pour tout (x,y) :
[edit]
J'ajouterai qu'ici ça n'est pas vraiment nécessaire, si on prend comme norme sur l'espace produit
La norme pour AxB est ici : |(x,y)| = racine de ( |x|² + |y|²).
Je vais essayé de comprendre pourquoi la continué est immediate avec la norme que tu as cité, et en faissant plus ou moins l'analogie avec celle ci-dessus je devrais y arrivé.
Mon probléme est plus maintenant de montré que ce sup existe et est fini, mais je devrais y arrivé.
Merci beaucoup
Je vais essayé de comprendre pourquoi la continué est immediate avec la norme que tu as cité, et en faissant plus ou moins l'analogie avec celle ci-dessus je devrais y arrivé.
Mon probléme est plus maintenant de montré que ce sup existe et est fini, mais je devrais y arrivé.
Merci beaucoup
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
