Montrer qu'un polynôme B divise un polynôme A
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 10 Jan 2021, 20:18
par mathelot » 10 Jan 2021, 20:18
on a: pour m,n entiers naturels
=T_{n+k}(Y))
(i) On va démontrer cette formule. Peux tu faire les calculs , @thoralf8weblen ?
(ii) Montrer que
=T_{0}(Y^{2^k}) \textrm{ avec } T_0(Y)=Y^2+Y+1)
(iii) Montrer que
)
divise
)
si
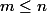 rappel de cours:
rappel de cours:^{2^m}=x^{2^n.2^m}=x^{2^{m+n}})
pour x réel, m et n entiers naturels
^2=X^{2^{n+1}})
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 11 Jan 2021, 23:01
par thoralf8weblen » 11 Jan 2021, 23:01
mathelot a écrit:Je conclus la 1ère étape:en résumé, quelque soit k entier naturel, j est racine de
=Y^{2^{k+1}}+Y^{2^{k}}+1)
Comme le polynôme
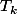
est à coefficients réels, et que

est le conjugué de j
alors si j est racine de
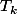
,

son conjugué est également racine de
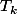
d'où
comme
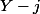
et
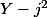
sont premiers entre eux,
(Y-j^2) =Y^2+Y+1)
divise
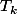
Je comprends la démarche sauf lorsque tu affirmes que
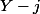
et
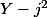
sont premiers entre eux. Je ne vois pas comment tu peux affirmer cela ni pourquoi tu as besoin d'affirmer cela.
Je serai tenté de dire que

et

sont deux racines de
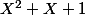
et
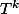
alors
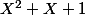
divise
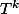
.
-
mathelot
 par mathelot » 11 Jan 2021, 23:22
par mathelot » 11 Jan 2021, 23:22
On utilise le théorème de Gauss:
si X-a et X-b divisent P et si X-a et X-b sont premiers entre eux,
alors (X-a)(X-b) divise P.
X-a divise P donc P s'écrit P(X)=(X-a)Q(X)
X-b divise P et X-b premier avec X-a alors X-b divise Q(X) (théorème de Gauss)
donc Q s'écrit Q(X)=(X-b)Q_1(X) d'où P(X)=(X-a)(X-b)Q_1(X)
Il n'aurait pas fallu que X-a et X-b aient un facteur commun non constant.
Modifié en dernier par mathelot le 12 Jan 2021, 12:30, modifié 2 fois.
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 11 Jan 2021, 23:24
par thoralf8weblen » 11 Jan 2021, 23:24
(i) On va démontrer cette formule. Peux tu faire les calculs , @thoralf8weblen ?
Bien sûr !
(ii) Montrer que
=T_{0}(Y^{2^k}) \textrm{ avec } T_0(Y)=Y^2+Y+1)
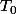
(Y^2^k)

(Y^2)^2^k+ Y^2^k
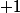
= Y^(2*2^k) + Y^2^k + 1
= Y^2^k+1 + Y^2^k + 1
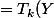)
(iii) Montrer que
)
divise
)
si
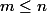
Je réfléchis...
-
mathelot
 par mathelot » 11 Jan 2021, 23:33
par mathelot » 11 Jan 2021, 23:33
j'ai rajouté des accolades
d'autre part on a:
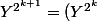^2)
Modifié en dernier par mathelot le 12 Jan 2021, 00:27, modifié 7 fois.
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 11 Jan 2021, 23:42
par thoralf8weblen » 11 Jan 2021, 23:42
d'autre part on a:
Y^(2^(k+1))=(Y^(2^k))^2
Je ne vois pas pourquoi tu fais ce rappel. Je pense que tu veux m'indiquer quelque chose mais je ne vois pas. Serait-ce en lien avec mon calcul précédent ? Il me semble correct.
-
mathelot
 par mathelot » 11 Jan 2021, 23:43
par mathelot » 11 Jan 2021, 23:43
mathelot a écrit: on a: pour m,n entiers naturels
=T_{n+k}(Y))
à démontrer!
-
mathelot
 par mathelot » 11 Jan 2021, 23:51
par mathelot » 11 Jan 2021, 23:51
thoralf8weblen a écrit: d'autre part on a:
Y^(2^(k+1))=(Y^(2^k))^2
Je ne vois pas pourquoi tu fais ce rappel. Je pense que tu veux m'indiquer quelque chose mais je ne vois pas. Serait-ce en lien avec mon calcul précédent ? Il me semble correct.
Tous les polynômes T_n ont une structure
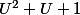
avec
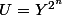
On a:
= Y^{2^{k+1}} + Y^{2^k}+1)
= Y^{2.2^k} + Y^{2^k}+1)
= (Y^{2^k} )^2+ Y^{2^k}+1)
=T_0(Y^{2^k}))
-
mathelot
 par mathelot » 12 Jan 2021, 12:09
par mathelot » 12 Jan 2021, 12:09
Soient m et n deux entiers naturels.
On suppose
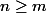
Montrons que
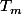
divise

=T_0(Y^{2^m}) \textrm{ avec } T_0(Y)=Y^2+Y+1)
)
divise
)
)
divise
)
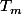
divise

-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 12 Jan 2021, 22:58
par thoralf8weblen » 12 Jan 2021, 22:58
mathelot a écrit:Soient m et n deux entiers naturels.
On suppose
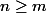
Montrons que
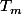
divise

=T_0(Y^{2^m}) \textrm{ avec } T_0(Y)=Y^2+Y+1)
)
divise
)
)
divise
)
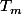
divise

J'ai du mal à comprendre ce que tu fais ici. Je pense que je ne comprends pas ce qui se passe au niveau des indices. Mon problème de compréhension vient de cette formule
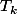
(Y^2^k)
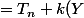)
J'ai repris ce que tu as fait de mon côté. Pour montrer que
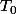
(Y^2^m) divise
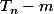
(Y^2^m), j'ai cherché à voir ce que valait ce polynôme. J'ai l'impression qu'il s'agit seulement d'un changement de lettre (m à la place de k).
Pour
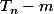
Y^2^m, je trouve (Y^2^m)^2 + Y^2^m + 1.
Qu'est-ce qui change entre l'indice 0 et l'indice n-m ?
-
Vassillia
 par Vassillia » 13 Jan 2021, 00:30
par Vassillia » 13 Jan 2021, 00:30
Bonsoir
Suite à la judicieuse proposition de GaBuZoMeu, il me semble que vous avez démontré après une lutte acharnée que
=Y^2+Y+1)
divise
)
, cette formule est valable pour tout

par exemple
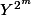
et pour tout

par exemple

Pourquoi avoir choisi
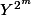
et

?
Et bien comme vu précédemment (pardon pour la formulation peu mathématiques) l'indice

en puissance va descendre pour faire disparaitre le

dans

et enfin nous donner le résultat attendu.
Plus rigoureusement, j'utilise
= Y^{2^{x+m+1}}+Y^{2^{x+m}}+1=Y^{2^m.2^{x+1}}+Y^{2^m.2^x}+1=({Y^{2^m}})^{2^{x+1}}+({Y^{2^m}})^{2^x}+1=T_x(Y^{2^m}))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 13 Jan 2021, 07:03
par GaBuZoMeu » 13 Jan 2021, 07:03
Je dirais plutôt
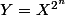
et
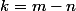
, en référence à l'énoncé et à mon premier message.

-
Vassillia
 par Vassillia » 13 Jan 2021, 10:22
par Vassillia » 13 Jan 2021, 10:22
Exact, j'avais répondu par rapport au message de mathelot.
Après une cinquantaine de messages, revenir à la question initiale est pertinent

-
mathelot
 par mathelot » 13 Jan 2021, 19:09
par mathelot » 13 Jan 2021, 19:09
mathelot a écrit:Soient m et n deux entiers naturels.
On suppose
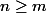
Montrons que
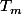
divise

=T_0(Y^{2^m}) \textrm{ avec } T_0(Y)=Y^2+Y+1)
=Y^{2^{m+1}}+Y^{2^{m}}+1=\left( Y^{2^m} \right)^{2}+Y^{2^m}+1=T_0(Y^{2^m}))
)
divise
)
En effet,
)
divise
)
donc, en changeant d'indéterminée
)
divise
)
= \left( Y^{2^m} \right)^{2^{n-m+1}} + \left( Y^{2^m} \right)^{2^{n-m}} +1)
= Y^{2^{m+n-m+1}} + Y^{2^{m+n-m}}+1)
= Y^{2^{n+1}}+Y^{2^n}+1)
=T_n(Y))
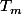
divise

.
ok , avec
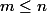 @thoralf8weblen
@thoralf8weblen Pour te repérer dans les indices et exposants, tu peux procéder ainsi:
= ?)
commence par écrire la variable du polynôme:
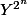
On fait agir T_m :
 ^{2^{m}})
on ajoute son carré
 ^{2^{m+1}})
qui est obtenu en incrémentant de 1 l'exposant externe
il vient:
 ^{2^{m+1}}+ \left( Y^{2^n} \right) ^{2^{m}}+1)
Modifié en dernier par mathelot le 13 Jan 2021, 21:34, modifié 1 fois.
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 13 Jan 2021, 21:31
par thoralf8weblen » 13 Jan 2021, 21:31
En effet,
)
divise
)
Cela me pose déjà problème. J'ai donc essayé de comprendre pourquoi
)
divise
)
.
On a démontré que
)
divise
)
. De plus les polynômes
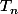
sont de la forme
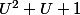
avec
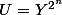
Donc
)
divise
)
car
)
divise tous les polynômes de la forme
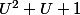
. Est-ce bien cela ?
Si cela est correct, alors je comprends qu'il suffit juste de changer l'indéterminée pour avoir:
)
divise
)
.
Sans problème
 = T_{0}(Y))
Il suffit simplement de changer la valeur de k et de l'indéterminée pour démontrer que
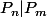
-
mathelot
 par mathelot » 13 Jan 2021, 21:51
par mathelot » 13 Jan 2021, 21:51
thoralf8weblen a écrit: En effet,
)
divise
)
Cela me pose déjà problème. J'ai donc essayé de comprendre pourquoi
)
divise
)
.
C'est ce que l'on a démontré avec les exposants modulo 3.
T_0 divise T_n pour tout entier n.
thoralf8weblen a écrit:Donc
)
divise
)
car
)
divise tous les polynômes de la forme
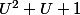
. Est-ce bien cela ?
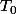
ne divise pas
^2+(Y+1)+1)
Si cela est correct, alors je comprends qu'il suffit juste de changer l'indéterminée pour avoir:
)
divise
)
.
Sans problème
 = T_{n}(Y))
Il suffit simplement de changer la valeur de k et de l'indéterminée pour démontrer que
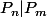
oui
Modifié en dernier par mathelot le 13 Jan 2021, 21:56, modifié 1 fois.
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 13 Jan 2021, 21:55
par thoralf8weblen » 13 Jan 2021, 21:55
thoralf8weblen a écrit: En effet,
)
divise
)
Cela me pose déjà problème. J'ai donc essayé de comprendre pourquoi
)
divise
)
.
On a démontré que
)
divise
)
. De plus les polynômes
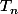
sont de la forme
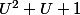
avec
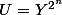
Donc
)
divise
)
car
)
divise tous les polynômes de la forme
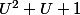
. Est-ce bien cela ?
Est-ce que ce raisonnement est correct du coup ?
mathelot a écrit:C'est ce que l'on a démontré avec les exposants modulo 3.
Justement, c'est cela que j'ai essayé de réemployer dans mon message précédent...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Jan 2021, 10:20
par GaBuZoMeu » 14 Jan 2021, 10:20
C'est vraiment interminable, ce fil !
On a vu que pour tout entier
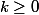
,
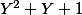
divise
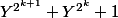
.
Soient
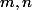
des entiers tels que
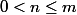
. Alors, en prenant
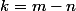
, on en déduit que
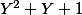
divise
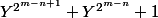
.
En faisant le changement de variable
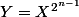
, on en déduit que
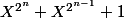
divise
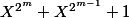
.
À titre d'exemple de calcul sur les puissances,
^{2^{m-n+1}} = X^{2^{n-1}\times2^{m-n+1}}= X^{2^{n-1+m-n+1}}=X^{2^m})
.
Et basta !
-
thoralf8weblen
- Membre Naturel
- Messages: 43
- Enregistré le: 11 Déc 2020, 17:24
-
 par thoralf8weblen » 14 Jan 2021, 21:19
par thoralf8weblen » 14 Jan 2021, 21:19
thoralf8weblen a écrit:Oui, tout à fait d'accord mais je manque de visibilité, c'est pour ça que je posais cette question. Ca ne me dit pas pourquoi tu as choisi X^2^(k+1).
Comme l'atteste cette citation présent dans les premiers messages, je t'ai demandé des éclairements que tu ne m'as jamais donnés. Ce n'est pas tes rares indications qui m'ont permis de comprendre la solution à cet exercice. Tu avais la solution dès le départ. Je ne comprends pas l'intérêt d'attendre plus de cinquante messages pour finalement se plaindre de la longueur de ce fil. Je pense avoir démontré mon implication. Je n'attends pas qu'on me donne la réponse. Cela ne m'intéresse pas. Je suis pugnace. Je n'abandonne jamais.
Alors oui, basta. Mais la prochaine fois, si c'est pour agir ainsi, je pense que tu pourras t'abstenir.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Jan 2021, 21:41
par GaBuZoMeu » 14 Jan 2021, 21:41
Il a fallu que j'insiste beaucoup et patiemment pour que tu comprennes enfin comment il fallait démontrer que
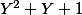
divise
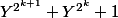
.
Après Mathelot a pris la main, et je l'ai laissé faire ... pas forcément de la façon dont j'aurais procédé.
Je t'avais suggéré dès le début le changement de variable
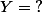
pour passer du cas particulier au cas général. Vassilia a été explicite quelques messages plus haut, et pourtant il me semble que ça continuait à patauger. C'est pourquoi j'ai jugé utile de mettre les points sur les i.
Bon, rien de grave. Si tu as finalement pu progresser dans ta compréhension c'est une bonne chose, et j'espère que tout est clair pour toi maintenant.
Modifié en dernier par
GaBuZoMeu le 14 Jan 2021, 21:53, modifié 1 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
est à coefficients réels, et que
est le conjugué de j
,
son conjugué est également racine de
et
sont premiers entre eux,
divise
divise
si
divise
divise
divise
divise
divise
divise
divise
.
divise
divise
divise
.
divise
car
divise tous les polynômes de la forme
. Est-ce bien cela ?
ne divise pas
divise
.
 = T_{n}(Y)) Il suffit simplement de changer la valeur de k et de l'indéterminée pour démontrer que
Il suffit simplement de changer la valeur de k et de l'indéterminée pour démontrer quedivise
divise
.
divise
. De plus les polynômes
sont de la forme
avec
divise
car
divise tous les polynômes de la forme
. Est-ce bien cela ?