Maths fi': calcul du prix d'une action
14 messages
- Page 1 sur 1
Maths fi': calcul du prix d'une action
Bonsoir,
j'ai lu pas mal de cours sur le sujet dont des PDF sur Internet, mais j'aimerais avoir confirmation de votre part car j'ai l'impression qu'il me manque des éléments nécessaires.
scénario (basé sur la méthode dite "actuarielle")
posons: div = dividende, 0 = année 0
div 0 = 10
on attend une croissance des dividendes de 3% sur les 6 prochaines années. Puis une croissance de 8%.
On souhaite conserver cet actif financier pour 10 ans (rentabilité exigée : 10%)
Méthode: alors, moi je connais la formule classique:
Prix 0 = D1/1+r + D2/(1+r)^2 + .... + (Dn + (Dn+1/r-g)) / (1+r)^(N)
mais là, on n'a pas besoin de Dn et Dn+1 puisqu'on ne cherche pas "à l'infini", la durée on la connait, elle est de 10 ans.
Donc sur Excel, j'aligne tous les dividendes, je les actualise au taux de rendement exigé (10%)
le hic c'est que je trouve en appliquant cette formule: P0 = 73.72
est-ce bon? car ce qui me chiffonne c'est que, là, le prix passe encore, mais si on met 16 ans, on arrive à 350 (au hasard) et sur 40 ans, certainement 800 et là on n'est plus du tout sur le prix d'une action réelle (chiffre très grand puisqu'on actualise un plus grand nombre de dividendes, tout simplement)
Donc où est-ce que je me plante dans ma formule ou la résolution de celle-ci? :mur:
Une fois qu'on a actualisé tous les flux attendus (= dividendes espérés), comment "réduire le chiffre de flux" pour arriver à trouver P0?
Merci d'avance!
j'ai lu pas mal de cours sur le sujet dont des PDF sur Internet, mais j'aimerais avoir confirmation de votre part car j'ai l'impression qu'il me manque des éléments nécessaires.
scénario (basé sur la méthode dite "actuarielle")
posons: div = dividende, 0 = année 0
div 0 = 10
on attend une croissance des dividendes de 3% sur les 6 prochaines années. Puis une croissance de 8%.
On souhaite conserver cet actif financier pour 10 ans (rentabilité exigée : 10%)
Méthode: alors, moi je connais la formule classique:
Prix 0 = D1/1+r + D2/(1+r)^2 + .... + (Dn + (Dn+1/r-g)) / (1+r)^(N)
mais là, on n'a pas besoin de Dn et Dn+1 puisqu'on ne cherche pas "à l'infini", la durée on la connait, elle est de 10 ans.
Donc sur Excel, j'aligne tous les dividendes, je les actualise au taux de rendement exigé (10%)
le hic c'est que je trouve en appliquant cette formule: P0 = 73.72
est-ce bon? car ce qui me chiffonne c'est que, là, le prix passe encore, mais si on met 16 ans, on arrive à 350 (au hasard) et sur 40 ans, certainement 800 et là on n'est plus du tout sur le prix d'une action réelle (chiffre très grand puisqu'on actualise un plus grand nombre de dividendes, tout simplement)
Donc où est-ce que je me plante dans ma formule ou la résolution de celle-ci? :mur:
Une fois qu'on a actualisé tous les flux attendus (= dividendes espérés), comment "réduire le chiffre de flux" pour arriver à trouver P0?
Merci d'avance!
Nicolas2012 a écrit:Bonsoir,
j'ai lu pas mal de cours sur le sujet dont des PDF sur Internet, mais j'aimerais avoir confirmation de votre part car j'ai l'impression qu'il me manque des éléments nécessaires.
scénario (basé sur la méthode dite "actuarielle")
posons: div = dividende, 0 = année 0
div 0 = 10
on attend une croissance des dividendes de 3% sur les 6 prochaines années. Puis une croissance de 8%.
On souhaite conserver cet actif financier pour 10 ans (rentabilité exigée : 10%)
Méthode: alors, moi je connais la formule classique:
Prix 0 = D1/1+r + D2/(1+r)^2 + .... + (Dn + (Dn+1/r-g)) / (1+r)^(N)
mais là, on n'a pas besoin de Dn et Dn+1 puisqu'on ne cherche pas "à l'infini", la durée on la connait, elle est de 10 ans.
Donc sur Excel, j'aligne tous les dividendes, je les actualise au taux de rendement exigé (10%)
le hic c'est que je trouve en appliquant cette formule: P0 = 73.72
est-ce bon? car ce qui me chiffonne c'est que, là, le prix passe encore, mais si on met 16 ans, on arrive à 350 (au hasard) et sur 40 ans, certainement 800 et là on n'est plus du tout sur le prix d'une action réelle (chiffre très grand puisqu'on actualise un plus grand nombre de dividendes, tout simplement)
Donc où est-ce que je me plante dans ma formule ou la résolution de celle-ci? :mur:
Une fois qu'on a actualisé tous les flux attendus (= dividendes espérés), comment "réduire le chiffre de flux" pour arriver à trouver P0?
Merci d'avance!
Bonsoir
Pour "essayer" de bien résoudre ce problème il faut procéder par étape et être "sur" des calculs intermédiaires.
QUESTION 1
Quels sont les montants de dividendes perçus au cours de 10 années ?
>QUESTION 1
>Quels sont les montants de dividendes perçus au cours de 10 années ?[/quote]
Bonsoir SAGE,
c'est effectivement par là que j'ai démarré, comme je l'ai écrit dans mon message. Je ne les écris pas tous mais pour commencer:
D1 = 10.30, D2 = 10.61, D3 = 10.93 (je les multiplie tous par 1.03)....
puis arrive D7 pour le nouveau taux de croissance = 12.90, puis D8 = 13.93....
j'ai actualisé D1, D2.... au taux de 10% et je trouve donc P0 = 73.72
donc une fois que ceci est fait. Une fois qu'on a cumulé les dividendes actualisés sur 10 ans, comment procède-t-on ensuite? Autrement dit, en te paraphrasant, quelle est la question 2?
Merci.
>Quels sont les montants de dividendes perçus au cours de 10 années ?[/quote]
Bonsoir SAGE,
c'est effectivement par là que j'ai démarré, comme je l'ai écrit dans mon message. Je ne les écris pas tous mais pour commencer:
D1 = 10.30, D2 = 10.61, D3 = 10.93 (je les multiplie tous par 1.03)....
puis arrive D7 pour le nouveau taux de croissance = 12.90, puis D8 = 13.93....
j'ai actualisé D1, D2.... au taux de 10% et je trouve donc P0 = 73.72
donc une fois que ceci est fait. Une fois qu'on a cumulé les dividendes actualisés sur 10 ans, comment procède-t-on ensuite? Autrement dit, en te paraphrasant, quelle est la question 2?
Merci.
Nicolas2012 a écrit:>QUESTION 1
>Quels sont les montants de dividendes perçus au cours de 10 années ?
Bonsoir SAGE,
c'est effectivement par là que j'ai démarré, comme je l'ai écrit dans mon message. Je ne les écris pas tous mais pour commencer:
D1 = 10.30, D2 = 10.61, D3 = 10.93 (je les multiplie tous par 1.03)....
puis arrive D7 pour le nouveau taux de croissance = 12.90, puis D8 = 13.93....
j'ai actualisé D1, D2.... au taux de 10% et je trouve donc P0 = 73.72
donc une fois que ceci est fait. Une fois qu'on a cumulé les dividendes actualisés sur 10 ans, comment procède-t-on ensuite? Autrement dit, en te paraphrasant, quelle est la question 2?
Merci.[/quote]
Je suis d'accord :
a) les dividendes bruts encaissés sur 10 ans sont de 124.73 euros
b) les dividendes actualisés sur 10 ans sont de 73.72 euros
Question 2 :
Pour percevoir CES dividendes
a) on a "payé" les actions quel montant, à l'époque "0" ?
b) quelle est la valeur des actions au bout de 10 ans ?
c) que doit-on faire des éléments au a) et b) ?
Bonsoir SAGE, je réponds à tes questions avant d'aller au lit:
b) quelle est la valeur des actions au bout de 10 ans ?
ça, c'est le premier problème! :ptdr:
Car sur un marché réel, en temps-réel, tu as P, le prix de l'actif financier. Ici, rien n'est dit dans l'énoncé, donc P0 (réel), je ne sais pas. Si on prends au rendement exigé, ça donne un coef multiplicateur:
X * (1.1)^10 = x2.5937X (arrondi) mais comme aucune indication, je ne vois pas comment calculer X, alias, P0.
a) on a "payé" les actions quel montant, à l'époque "0" ?
là aussi, comme P0 = X = inconnu et comme la formule P0, elle est écrite dans mon 1er message, je ne vois pas quoi répondre de plus surtout avec P10 inconnu puisqu'aucune indication sur P0... :mur:
c) que doit-on faire des éléments au a) et b) ?
A priori, je dirais les actualiser. ça consisterait à reprendre tous les flux attendus (plus value + hausse du dividende) sur chaque année, et hop, on envoit tout ça à l'actualisation au taux de rendement exigé et roule Emile... le hic c'est que pour répondre à tes questions, j'ai P10 = 2.5937X, j'suis bien avancé avec ça... et la a/ je ne vois pas quoi te répondre... je pensais que la formule était DEJA complète...
nan, il faut que tu me donnes d'autres indices, je le crains :marteau:
Merci et bonne nuit!
b) quelle est la valeur des actions au bout de 10 ans ?
ça, c'est le premier problème! :ptdr:
Car sur un marché réel, en temps-réel, tu as P, le prix de l'actif financier. Ici, rien n'est dit dans l'énoncé, donc P0 (réel), je ne sais pas. Si on prends au rendement exigé, ça donne un coef multiplicateur:
X * (1.1)^10 = x2.5937X (arrondi) mais comme aucune indication, je ne vois pas comment calculer X, alias, P0.
a) on a "payé" les actions quel montant, à l'époque "0" ?
là aussi, comme P0 = X = inconnu et comme la formule P0, elle est écrite dans mon 1er message, je ne vois pas quoi répondre de plus surtout avec P10 inconnu puisqu'aucune indication sur P0... :mur:
c) que doit-on faire des éléments au a) et b) ?
A priori, je dirais les actualiser. ça consisterait à reprendre tous les flux attendus (plus value + hausse du dividende) sur chaque année, et hop, on envoit tout ça à l'actualisation au taux de rendement exigé et roule Emile... le hic c'est que pour répondre à tes questions, j'ai P10 = 2.5937X, j'suis bien avancé avec ça... et la a/ je ne vois pas quoi te répondre... je pensais que la formule était DEJA complète...
nan, il faut que tu me donnes d'autres indices, je le crains :marteau:
Merci et bonne nuit!
Bonsoir,
Je ne suis pas d'accord avec certains points qui ont été énoncés.
Cette formule est en fait un "2-stage dividend discount model" et ne doit s'appliquer que sous l'hypothèse d'une croissance infinie au second stage.
Je m'explique en reprenant depuis le début en essayant d'être bref, sans trop l'être non plus.
Pour déterminer le prix d'une action d'une entreprise versant actuellement un dividende (et qui est supposée verser des dividendes dans le futur ou non), les "dividend discount model" (DDM) sont généralement utilisés et notamment le "Gordon Growth Model" (ou Gordon Shapiro en français / Shapiro n'apparaissant nul part dans la littérature anglo-saxonne...).
Pour un actionnaire, il existe deux types de cash-flows:
1) les dividendes futurs
2) le prix de vente futur
La formule permettant de calculer le prix d'une action (avec un horizon fixé) avec un DDM est la suivante:
^t} + \frac{Pn}{(1+r)^n})
^n}) est appelée la "Terminal Value", il s'agit du prix de vente estimé actualisé.
est appelée la "Terminal Value", il s'agit du prix de vente estimé actualisé.
Le Gordon Growth Model est un cas particulier des dividend discount model, il suppose que les dividendes ont une croissance constante à travers le temps, la formule devient ainsi :
^t}{(1+r)^t}) avec:
avec:
- n tendant vers l'infini
- g le taux de croissance des dividendes
- r la rentabilité exigée
De ce fait, on obtient (après factorisation par D0, puis série géométrique à l'infini):
- si r > g :}{(r-g)} = \frac{D1}{(r-g)})
- si g = 0 :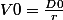
Considérons maintenant plusieurs taux de croissance de dividendes ("multi stage DDM"):
^t}{(1+r)^t}+\frac{Vn}{(1+r)^n})
Mais comme Vn est la Terminal Value fixée par le Gordon Growth Model, on peut écrire :
})
avec^n(1+g2))
==> on retrouve en fait ici ta formule, qui est en fait une croissance à l'infini avec le r-g2 (voir plus haut)
Il n'est possible d'utiliser que les dividendes que lorsque l'on suppose un horizon infini. Si l'horizon est donné (ici, 10 ans), il faut un prix de vente estimé en guise de "valeur de sortie".
Cette affirmation est fausse lorsque l'horizon est infini. Le prix de l'action est insensible que l'on sorte dans 5 ans, dans 10 ou dans 15 ans.
Les DDM sont extrêmement sensibles aux paramètres r et g. L'exemple que tu donnes est je dois l'avouer très peu intuitif puisque les multi-stage DDM sont généralement utilisés pour représenter les différents cycles de croissance d'une entreprise ==> le premier taux de croissance du dividende est généralement le plus élevé, la dernière phase (représentant la phase de maturité de l'entreprise) devrait avoir un taux de croissance plus faible.
Exemple d'utilisation d'un 2 stage DDM :
Soit D0 = 5, 10% de croissance de dividendes pour les 3 premières années, 5% ensuite. Rendement exigé 15%.
On a :
D1 = 5 * 1.1 = 5.50
D2 = 6.05
D3 = 6.655
D4 = D0(1+0.1)^3(1+0.05)=6.98775
V3 = 6.98775 / (0.15-0.05) = 69.8775
On actualise D1,D2,D3 et V3, on obtient : 59.68.
Dans ton cas :
- soit il faut considérer une croissance infinie à partir de la 6ème année pour pouvoir utiliser la formule que tu as pris (le résultat sera élevé, vu que la différence r-g sera faible, vu que ton g est contre intuitivement trop élevé)
- soit avoir un prix de vente estimé en guise de terminal value (on ne peut pas se restreindre à des dividendes comme cash flow)
PS: je ne me connecte que la nuit et ne passerai que demain soir
Bonne soirée.
Je ne suis pas d'accord avec certains points qui ont été énoncés.
Nicolas2012 a écrit: Prix 0 = D1/1+r + D2/(1+r)^2 + .... + (Dn + (Dn+1/r-g)) / (1+r)^(N)
Cette formule est en fait un "2-stage dividend discount model" et ne doit s'appliquer que sous l'hypothèse d'une croissance infinie au second stage.
Je m'explique en reprenant depuis le début en essayant d'être bref, sans trop l'être non plus.
Pour déterminer le prix d'une action d'une entreprise versant actuellement un dividende (et qui est supposée verser des dividendes dans le futur ou non), les "dividend discount model" (DDM) sont généralement utilisés et notamment le "Gordon Growth Model" (ou Gordon Shapiro en français / Shapiro n'apparaissant nul part dans la littérature anglo-saxonne...).
Pour un actionnaire, il existe deux types de cash-flows:
1) les dividendes futurs
2) le prix de vente futur
La formule permettant de calculer le prix d'une action (avec un horizon fixé) avec un DDM est la suivante:
Le Gordon Growth Model est un cas particulier des dividend discount model, il suppose que les dividendes ont une croissance constante à travers le temps, la formule devient ainsi :
- n tendant vers l'infini
- g le taux de croissance des dividendes
- r la rentabilité exigée
De ce fait, on obtient (après factorisation par D0, puis série géométrique à l'infini):
- si r > g :
- si g = 0 :
Considérons maintenant plusieurs taux de croissance de dividendes ("multi stage DDM"):
Mais comme Vn est la Terminal Value fixée par le Gordon Growth Model, on peut écrire :
avec
==> on retrouve en fait ici ta formule, qui est en fait une croissance à l'infini avec le r-g2 (voir plus haut)
Il n'est possible d'utiliser que les dividendes que lorsque l'on suppose un horizon infini. Si l'horizon est donné (ici, 10 ans), il faut un prix de vente estimé en guise de "valeur de sortie".
Nicolas2012 a écrit:car ce qui me chiffonne c'est que, là, le prix passe encore, mais si on met 16 ans, on arrive à 350 (au hasard) et sur 40 ans, certainement 800 et là on n'est plus du tout sur le prix d'une action réelle (chiffre très grand puisqu'on actualise un plus grand nombre de dividendes, tout simplement)
Cette affirmation est fausse lorsque l'horizon est infini. Le prix de l'action est insensible que l'on sorte dans 5 ans, dans 10 ou dans 15 ans.
Les DDM sont extrêmement sensibles aux paramètres r et g. L'exemple que tu donnes est je dois l'avouer très peu intuitif puisque les multi-stage DDM sont généralement utilisés pour représenter les différents cycles de croissance d'une entreprise ==> le premier taux de croissance du dividende est généralement le plus élevé, la dernière phase (représentant la phase de maturité de l'entreprise) devrait avoir un taux de croissance plus faible.
Exemple d'utilisation d'un 2 stage DDM :
Soit D0 = 5, 10% de croissance de dividendes pour les 3 premières années, 5% ensuite. Rendement exigé 15%.
On a :
D1 = 5 * 1.1 = 5.50
D2 = 6.05
D3 = 6.655
D4 = D0(1+0.1)^3(1+0.05)=6.98775
V3 = 6.98775 / (0.15-0.05) = 69.8775
On actualise D1,D2,D3 et V3, on obtient : 59.68.
Dans ton cas :
- soit il faut considérer une croissance infinie à partir de la 6ème année pour pouvoir utiliser la formule que tu as pris (le résultat sera élevé, vu que la différence r-g sera faible, vu que ton g est contre intuitivement trop élevé)
- soit avoir un prix de vente estimé en guise de terminal value (on ne peut pas se restreindre à des dividendes comme cash flow)
PS: je ne me connecte que la nuit et ne passerai que demain soir
Bonne soirée.
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
M. Twain
maxnihilist a écrit:Bonsoir,
Je ne suis pas d'accord avec certains points qui ont été énoncés.
Cette formule est en fait un "2-stage dividend discount model" et ne doit s'appliquer que sous l'hypothèse d'une croissance infinie au second stage.
Je m'explique en reprenant depuis le début en essayant d'être bref, sans trop l'être non plus.
Pour déterminer le prix d'une action d'une entreprise versant actuellement un dividende (et qui est supposée verser des dividendes dans le futur ou non), les "dividend discount model" (DDM) sont généralement utilisés et notamment le "Gordon Growth Model" (ou Gordon Shapiro en français / Shapiro n'apparaissant nul part dans la littérature anglo-saxonne...).
Pour un actionnaire, il existe deux types de cash-flows:
1) les dividendes futurs
2) le prix de vente futur
La formule permettant de calculer le prix d'une action (avec un horizon fixé) avec un DDM est la suivante:est appelée la "Terminal Value", il s'agit du prix de vente estimé actualisé.
Le Gordon Growth Model est un cas particulier des dividend discount model, il suppose que les dividendes ont une croissance constante à travers le temps, la formule devient ainsi :avec:
- n tendant vers l'infini
- g le taux de croissance des dividendes
- r la rentabilité exigée
De ce fait, on obtient (après factorisation par D0, puis série géométrique à l'infini):
- si r > g :
- si g = 0 :
Considérons maintenant plusieurs taux de croissance de dividendes ("multi stage DDM"):
Mais comme Vn est la Terminal Value fixée par le Gordon Growth Model, on peut écrire :})
avec
==> on retrouve en fait ici ta formule, qui est en fait une croissance à l'infini avec le r-g2 (voir plus haut)
Il n'est possible d'utiliser que les dividendes que lorsque l'on suppose un horizon infini. Si l'horizon est donné (ici, 10 ans), il faut un prix de vente estimé en guise de "valeur de sortie".
Cette affirmation est fausse lorsque l'horizon est infini. Le prix de l'action est insensible que l'on sorte dans 5 ans, dans 10 ou dans 15 ans.
Les DDM sont extrêmement sensibles aux paramètres r et g. L'exemple que tu donnes est je dois l'avouer très peu intuitif puisque les multi-stage DDM sont généralement utilisés pour représenter les différents cycles de croissance d'une entreprise ==> le premier taux de croissance du dividende est généralement le plus élevé, la dernière phase (représentant la phase de maturité de l'entreprise) devrait avoir un taux de croissance plus faible.
Exemple d'utilisation d'un 2 stage DDM :
Soit D0 = 5, 10% de croissance de dividendes pour les 3 premières années, 5% ensuite. Rendement exigé 15%.
On a :
D1 = 5 * 1.1 = 5.50
D2 = 6.05
D3 = 6.655
D4 = D0(1+0.1)^3(1+0.05)=6.98775
V3 = 6.98775 / (0.15-0.05) = 69.8775
On actualise D1,D2,D3 et V3, on obtient : 59.68.
Dans ton cas :
- soit il faut considérer une croissance infinie à partir de la 6ème année pour pouvoir utiliser la formule que tu as pris (le résultat sera élevé, vu que la différence r-g sera faible, vu que ton g est contre intuitivement trop élevé)
- soit avoir un prix de vente estimé en guise de terminal value (on ne peut pas se restreindre à des dividendes comme cash flow)
PS: je ne me connecte que la nuit et ne passerai que demain soir
Bonne soirée.
Bonjour à tous
MAXNIHILIST a donné une réponse plus complète que celle que j'aurais pu proposée.
Nous parlons, ici, d'actions et donc de société, d'entreprise et de .....bilan.
Or établir un bilan "SINCERE et VERITABLE" est un travail de longue haleine : comptable, expert-comptable, commissaires aux comptes, conseillers juridiques, conseillers fiscaux, et ...., et.....
Et, quant on a un bilan "exact" à une date précise, il fait EXTRAPOLER l'AVENIR....et sans l'aide de la boule magique.....la difficulté commence pour "EVALUER" une entreprise.
Plusieurs méthode de calculs existent, il faut faire la synthèse, quelques fois prendre une partie de l'une, une partie de l'autre et conclure suivant les éléments que l'on a.
Max et SAGE, bonne et heureuse Année et surtout merci beaucoup les gars!
Effectivement SAGE, Max a répondu de manière très exhaustive à la question, tout comme toi, je n'en attendais pas autant, clairement :ptdr: (et merci, j'ai bien ri aussi sur les anecdotes anglo-saxonnes fort intéressantes)
alors maintenant, de mon côté, j'ai continué à étudier et chercher des pistes de réflexions grâce à vos commentaires et corrections... je vous avoue qu'avant de trouver "le Graal", j'en étais resté à la formule barbare suivante:
P0 = D1/r-g1 (1-(1+g1/1+r)^4) + [(D1(1+g1)^(4)/r-g2](1+r)^(4)
mais bizarrement... je la trouvais un brin... abscons LOL :zen:
donc, j'ai continué, et je suis tombé sur une méthode très intéressante, dite "à reculons", ou grâce à la formule simple suivante: Pt-1 = Dt / (r-g), tu vas chercher en fait le prix de l'action à un instant T, grâce à T+1 "à reculons"
malheureusement, in fine, tu reviens sur la formule barbare du dessus pour aller jusqu'à T0
et donc, j'ai continué! et là j'ai trouvé quelque chose qui a nettement plus de sens et nettement plus praticable pour moi. Je vous donne un exemple:
"on sait que le div de l'année prochaine sera de 100", "de T1 à T5 (donc attention à ne PAS oublier de rentrer T1 = 100 dans la formule!), g = 15%, puis on passe à 2% à partir de T6"
eh bien, tout simplement (même si ça rejoint la formule de Pt-1 mais en nettement plus limpide quand même):
D1 = 100
D2 = 115
...
D5 = 174.90
D6 = 178.40 (qu'on doit avoir pour calculer le prix de D5)
P(T5) = (178.40) / (0.1 - 0.02 ) = 2 230
et c'est là où ça devient génial car extrêmement logique, tout simplement, on actualise D1 jusqu'à D5 ET! on actualise 2 230 sur T5 (en oubliant 178.40, normal)
résultat: P0 = 1 882
j'adore cette technique, que je trouve beaucoup plus praticable que la formule de l'espace n°1 sur laquelle on a le temps de se tromper 20x avant de trouver le bon chiffre :lol3:
et les gars, Max et SAGE, merci encore pour vos réponses si détaillées, y'a beaucoup à prendre sur chacune, c'est cool. Bonne fin de WE à vous.
Effectivement SAGE, Max a répondu de manière très exhaustive à la question, tout comme toi, je n'en attendais pas autant, clairement :ptdr: (et merci, j'ai bien ri aussi sur les anecdotes anglo-saxonnes fort intéressantes)
alors maintenant, de mon côté, j'ai continué à étudier et chercher des pistes de réflexions grâce à vos commentaires et corrections... je vous avoue qu'avant de trouver "le Graal", j'en étais resté à la formule barbare suivante:
P0 = D1/r-g1 (1-(1+g1/1+r)^4) + [(D1(1+g1)^(4)/r-g2](1+r)^(4)
mais bizarrement... je la trouvais un brin... abscons LOL :zen:
donc, j'ai continué, et je suis tombé sur une méthode très intéressante, dite "à reculons", ou grâce à la formule simple suivante: Pt-1 = Dt / (r-g), tu vas chercher en fait le prix de l'action à un instant T, grâce à T+1 "à reculons"
malheureusement, in fine, tu reviens sur la formule barbare du dessus pour aller jusqu'à T0
et donc, j'ai continué! et là j'ai trouvé quelque chose qui a nettement plus de sens et nettement plus praticable pour moi. Je vous donne un exemple:
"on sait que le div de l'année prochaine sera de 100", "de T1 à T5 (donc attention à ne PAS oublier de rentrer T1 = 100 dans la formule!), g = 15%, puis on passe à 2% à partir de T6"
eh bien, tout simplement (même si ça rejoint la formule de Pt-1 mais en nettement plus limpide quand même):
D1 = 100
D2 = 115
...
D5 = 174.90
D6 = 178.40 (qu'on doit avoir pour calculer le prix de D5)
P(T5) = (178.40) / (0.1 - 0.02 ) = 2 230
et c'est là où ça devient génial car extrêmement logique, tout simplement, on actualise D1 jusqu'à D5 ET! on actualise 2 230 sur T5 (en oubliant 178.40, normal)
résultat: P0 = 1 882
j'adore cette technique, que je trouve beaucoup plus praticable que la formule de l'espace n°1 sur laquelle on a le temps de se tromper 20x avant de trouver le bon chiffre :lol3:
et les gars, Max et SAGE, merci encore pour vos réponses si détaillées, y'a beaucoup à prendre sur chacune, c'est cool. Bonne fin de WE à vous.
Re,
je tiens à préciser que "mon" modèle n'est valable QUE pour "croissance à l'infini", si on prend 5, 10 ou X année, il faut repasser par la formule barbare quand même :doh:
et oui Max, en te relisant et en faisant différents calculs pour tester, j'ai compris pourquoi la période de conservation de l'actif importe peu... c'est plein de bon sens comme dirait nos amis québécois, car si on prend la formule "barbare", tout ce qui se passe en aval n'a aucune incidence sur le prix, logique.
réglé! :we:
je tiens à préciser que "mon" modèle n'est valable QUE pour "croissance à l'infini", si on prend 5, 10 ou X année, il faut repasser par la formule barbare quand même :doh:
et oui Max, en te relisant et en faisant différents calculs pour tester, j'ai compris pourquoi la période de conservation de l'actif importe peu... c'est plein de bon sens comme dirait nos amis québécois, car si on prend la formule "barbare", tout ce qui se passe en aval n'a aucune incidence sur le prix, logique.
réglé! :we:
Bonjour,
Tout cela me parait être dans le bon sens.
Petite remarque tout de même :
et
Ainsi que :
se réfère à la même méthode. C'est simplement un premier stage jusqu'à une année donnée, puis un second stage à l'infini.
PS: dans ton exemple, tu utilises un taux de croissance à l'infini de 2%, ce qui est déjà bien plus intuitif que l'exemple initial.
A titre indicatif, certains cabinets d'affaires (M&A etc.) n'hésite pas à utiliser les "forecasts" de la croissance mondiale pour fixer le paramètre g à l'infini (source: rapport de l'AMF). Plutôt que d'utiliser la formule habituelle de g (taux de rétention multiplié par le return on equity). On considère la croissance mondiale comme un moteur; et il est difficile d'imaginer une entreprise "battre" son propre moteur sur le long terme.
Bon week-end
Tout cela me parait être dans le bon sens.
Petite remarque tout de même :
maxnihilist a écrit:
Exemple d'utilisation d'un 2 stage DDM :
Soit D0 = 5, 10% de croissance de dividendes pour les 3 premières années, 5% ensuite. Rendement exigé 15%.
On a :
D1 = 5 * 1.1 = 5.50
D2 = 6.05
D3 = 6.655
D4 = D0(1+0.1)^3(1+0.05)=6.98775
V3 = 6.98775 / (0.15-0.05) = 69.8775
On actualise D1,D2,D3 et V3, on obtient : 59.68.
et
Nicolas2012 a écrit:
Je vous donne un exemple:
"on sait que le div de l'année prochaine sera de 100", "de T1 à T5 (donc attention à ne PAS oublier de rentrer T1 = 100 dans la formule!), g = 15%, puis on passe à 2% à partir de T6"
eh bien, tout simplement (même si ça rejoint la formule de Pt-1 mais en nettement plus limpide quand même):
D1 = 100
D2 = 115
...
D5 = 174.90
D6 = 178.40 (qu'on doit avoir pour calculer le prix de D5)
P(T5) = (178.40) / (0.1 - 0.02 ) = 2 230
et c'est là où ça devient génial car extrêmement logique, tout simplement, on actualise D1 jusqu'à D5 ET! on actualise 2 230 sur T5 (en oubliant 178.40, normal)
résultat: P0 = 1 882
Ainsi que :
maxnihilist a écrit:
Considérons maintenant plusieurs taux de croissance de dividendes ("multi stage DDM"):
Mais comme Vn est la Terminal Value fixée par le Gordon Growth Model, on peut écrire :
avec
se réfère à la même méthode. C'est simplement un premier stage jusqu'à une année donnée, puis un second stage à l'infini.
PS: dans ton exemple, tu utilises un taux de croissance à l'infini de 2%, ce qui est déjà bien plus intuitif que l'exemple initial.
A titre indicatif, certains cabinets d'affaires (M&A etc.) n'hésite pas à utiliser les "forecasts" de la croissance mondiale pour fixer le paramètre g à l'infini (source: rapport de l'AMF). Plutôt que d'utiliser la formule habituelle de g (taux de rétention multiplié par le return on equity). On considère la croissance mondiale comme un moteur; et il est difficile d'imaginer une entreprise "battre" son propre moteur sur le long terme.
Bon week-end
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
M. Twain
Bonsoir Max, pourquoi n'ai-je pas reçu d'avertissement par mail que tu avais posté une nouvelle réponse??? Bref...
>A titre indicatif, certains cabinets d'affaires (M&A etc.) n'hésite pas à utiliser les "forecasts" de la >croissance mondiale pour fixer le paramètre g à l'infini (source: rapport de l'AMF). Plutôt que >d'utiliser la formule habituelle de g (taux de rétention multiplié par le return on equity). On considère >la croissance mondiale comme un moteur; et il est difficile d'imaginer une entreprise "battre" son >propre moteur sur le long terme.
SUPER intéressant, ça je garde :lol3:
Bonne soirée,
Nicolas
>A titre indicatif, certains cabinets d'affaires (M&A etc.) n'hésite pas à utiliser les "forecasts" de la >croissance mondiale pour fixer le paramètre g à l'infini (source: rapport de l'AMF). Plutôt que >d'utiliser la formule habituelle de g (taux de rétention multiplié par le return on equity). On considère >la croissance mondiale comme un moteur; et il est difficile d'imaginer une entreprise "battre" son >propre moteur sur le long terme.
SUPER intéressant, ça je garde :lol3:
Bonne soirée,
Nicolas
Bonsoir,
Le taux de rétention est la proportion du résultat net qui n'est pas redistribué sous forme de dividendes : (résultat net - dividendes)/résultat net
On peut aussi l'exprimer en fonction du payout ratio:
Retention rate = 1 - payout ratio (ratio de distribution)
payout ratio = dividend per share (dividende par action) / earnings per share (benefice par action)
Le taux de rétention est la proportion du résultat net qui n'est pas redistribué sous forme de dividendes : (résultat net - dividendes)/résultat net
On peut aussi l'exprimer en fonction du payout ratio:
Retention rate = 1 - payout ratio (ratio de distribution)
payout ratio = dividend per share (dividende par action) / earnings per share (benefice par action)
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
M. Twain
>Le taux de rétention est la proportion du résultat net qui n'est pas redistribué sous forme de >dividendes : (résultat net - dividendes)/résultat net
>On peut aussi l'exprimer en fonction du payout ratio:
>Retention rate = 1 - payout ratio (ratio de distribution)
>payout ratio = dividend per share (dividende par action) / earnings per share (benefice par action)
Toujours au TOP Max! Merci beaucoup pour ces quelques éclaircissements, tout est limpide maintenant :ptdr:
Je creuserai tout ça quand j'aurai le temps. Bonne journée!
>On peut aussi l'exprimer en fonction du payout ratio:
>Retention rate = 1 - payout ratio (ratio de distribution)
>payout ratio = dividend per share (dividende par action) / earnings per share (benefice par action)
Toujours au TOP Max! Merci beaucoup pour ces quelques éclaircissements, tout est limpide maintenant :ptdr:
Je creuserai tout ça quand j'aurai le temps. Bonne journée!
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
