Soit H un anneau (groupe commutatif + multiplication Z-linéaire) tel que
\rightarrow (H,.))
\rightarrow (H,.))
ps : pour H = Z[X], f envoit n sur X^{n+1} car 0 s'envoit sur X.
Le morphisme f induit une action de N sur H. Montrons que, on a
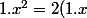=2x^{2})
,
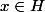
. (et
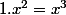
donc contradiction)
La multiplication est donné par le morphisme
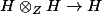
par conséquent n.x² = n. (x\otimes x) en considérant l'action de N sur
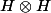
.
Il existe une seule action (à isomorphisme près) sur
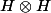
tel que les deux morphismes "d'inclusion" de H dans
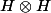
soit N-linéaire.
Là faudrait faire un diagramme, je vais expliquer sans.
Les deux morphismes N-linéaires de H dans
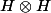
induisent deux morphismes de H dans la somme directe de
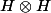
avec lui-même. Le morphisme naturel de la somme directe dans
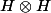
est l'addition.
On obtient donc que
)
est image par addition de
\oplus(x\otimes 1.x))
Soit
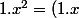x+x(1.x) = 2x(1.x) = 2x^{2})
.
