Tu as raison formellement, une application est souvent définie comme la donnée d'un triplet formé de l'ensemble de départ, de l'ensemble d'arrivée et du graphe (sous-ensemble du produit cartésien des deux).
Si on augmente l'ensemble de départ sans changer le reste, ce n'est plus une application.
Si on augmente l'ensemble d'arrivée sans changer le reste, c'est toujours une application. Pas la même, d'accord, on peut d'ailleurs perdre des propriétés comme la surjectivité. Mais on commet souvent l'abus de l'appeler du même nom, et dans tous les cas évoqués dans ce fil ça ne pose pas vraiment de problème : pas de problème quand on parle de la limite, et quand on parle de convergence, il convient bien sûr de préciser là où on se place (dans
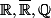
...).
Tu sembles poser la question du pourquoi dans la définition 1.69 de limite on parle d'un sous-ensemble

de l'espace

et pas d'un sous-ensemble

de l'espace

. Tout simplement parce que ça n'apporterait rien (une application arrivant dans

peut canoniquement être considérée comme arrivant dans

) tandis que c'est indispensable de parler de

(une application définie sur

ne peut pas être considérée comme définie sur

). Et pour parler de limite de

en

il est bien sûr nécessaire d'avoir

dans l'adhérence du domaine de définition de

.
Histoire de t'embrouiller, un petit exemple. Soit
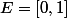
et soit

le recollement de deux copies de

le long de
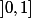
. Autrement dit,

est

où on a dédoublé le point

en deux points
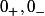
. Une base de voisinages de
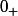
dans

est formée des
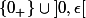
pour
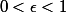
, avec l'analogue pour
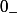
.
Prenons
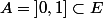
et
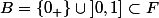
, et
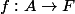
définie par
=x)
. La fonction

est à valeurs dans

et se prolonge par continuité en

en une fonction à valeurs dans

, mais elle a aussi une limite en

qui n'appartient pas à

.



