Intégration : dx variable
42 messages
- Page 1 sur 3 - 1, 2, 3
Bon, alors je le reformule mieux :
si x est une fonction continue croissante sur [a,b] alors :
}^{x(b)} f(t)\, dt = \lim_{N \to \infty}\sum_{n=0}^{N-1} [x( a + (n+1) \frac{b-a}{N} ) - x( a + n \frac{b-a}{N} )] * f ( x ( a + n \frac{b-a}{N} ) ))
 \frac{b-a}{N}-x( a + n \frac{b-a}{N}] ) * f ( x ( a + n \frac{b-a}{N} ) ))
Chimono, c'est juste ? Parce que tu es meilleur que moi .. même si tu m'énerves
Bon, et est-ce-que ca te satisfait cette définition plus générale ?
On peut retrouver ainsi la formule du changement de variable :
}^{x(b)} f(t)\, dt = \lim_{N \to \infty}\sum_{n=0}^{N-1} [x( a + (n+1) \frac{b-a}{N}-x( a + n \frac{b-a}{N}] * f ( x ( a + n \frac{b-a}{N} ) ))
Maintenant, faisons apparaitre dt=(b-a)/N afin de retrouver une série de Rieman :
 \frac{b-a}{N}-x( a + n \frac{b-a}{N}]}{\frac{b-a}{N}} * f ( x ( a + n \frac{b-a}{N} ) ))
Donc, d'après la définition de la dérivée et la définition de l'intégrale selon Rieman :
*f(x(t))\, dt)
Tout cela me parait peu historique...
Non ?
Jean
si x est une fonction continue croissante sur [a,b] alors :
Chimono, c'est juste ? Parce que tu es meilleur que moi .. même si tu m'énerves
Bon, et est-ce-que ca te satisfait cette définition plus générale ?
On peut retrouver ainsi la formule du changement de variable :
Maintenant, faisons apparaitre dt=(b-a)/N afin de retrouver une série de Rieman :
Donc, d'après la définition de la dérivée et la définition de l'intégrale selon Rieman :
Tout cela me parait peu historique...
Non ?
Jean
Bon, donc finalement, j'ai obtenu la formule du changement de variable en disant que pour l'intégrale de a à b de f(x)dx, dx povait varier , mais pour que l'intégrale soit bien de a à b, il fallait que x(a)=a et x(b)=b
Mais on se rend compte que si x(a)=i et x(b)=j, on a tout simplement l'intégrale de f(x)dx de i à j ....
On trouve alors la formule plus générale qui nous permet ensuite de trouver la formule du changement de variable.
Jean
Mais on se rend compte que si x(a)=i et x(b)=j, on a tout simplement l'intégrale de f(x)dx de i à j ....
On trouve alors la formule plus générale qui nous permet ensuite de trouver la formule du changement de variable.
Jean
J'ai ne vois pas bien ce que tu veux montrer. Est-ce que tu veux faire un changement de variable dans la somme de Riemann ?
Et je n'ai pas très bien compris le}^{x(b)} f(t)\, dt = \lim_{N \to \infty}\sum_{n=0}^{N-1} [x( a + (n+1) \frac{b-a}{N} ) - x( a + n \frac{b-a}{N} )] * f ( x ( a + n \frac{b-a}{N} ) ))
Voilà si tu pouvais m'expliquer
Quand on fait un CDV x=g(t) on a effictivement un dx variable, égal à g'(t)dt
Après on fait la somme pour x variant de a à b, donc t varie de c=g-1(a) à d=g-1(b)
Je pense qu'après on doit faire la somme de f(x)dx avec dx = g'(c + k(d-c)/n) * (d-c)/n
Mais on trouve quelque chose d'assez compliqué.
Et je n'ai pas très bien compris le
Voilà si tu pouvais m'expliquer
Quand on fait un CDV x=g(t) on a effictivement un dx variable, égal à g'(t)dt
Après on fait la somme pour x variant de a à b, donc t varie de c=g-1(a) à d=g-1(b)
Je pense qu'après on doit faire la somme de f(x)dx avec dx = g'(c + k(d-c)/n) * (d-c)/n
Mais on trouve quelque chose d'assez compliqué.
Ce qui me prait sympa avec cette formule générale, c'est que toute fonction y continue croissante sur a,b telle que y(a)=x(a) et y(b)=x(b) peut prendre la place de la fonction x ....
Ainsi ... Par exemple : On peut placer l'intégrale sur n'importe quel intervalle !!!
Soit\, dx)
Imaginons qu'on veuille se placer sur l'intervalle [0,1]
Soit = cx + d)
=a=d)
D'où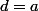
=b=c+a)
Donc c=b-a
Donc}^{y(1)} f(x)\, dx = \lim_{N \to \infty}\sum_{n=0}^{N-1} dy(n/N)*f(y(n/N)) = \int_{0}^{1} y'(t)*f(y(t))\, dt)
Donc*\int_{0}^{1} f(y(x))\, dx)
On peut obtenir ainsi par exemple :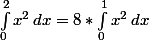
ou encore :
\, dx = 2*\int_{0}^{1} exp(2x)\, dx)
Voili Voilo
Jean
Ainsi ... Par exemple : On peut placer l'intégrale sur n'importe quel intervalle !!!
Soit
Imaginons qu'on veuille se placer sur l'intervalle [0,1]
Soit
D'où
Donc c=b-a
Donc
Donc
On peut obtenir ainsi par exemple :
ou encore :
Voili Voilo
Jean
Imaginons qu'on veuille intégrer f sur x(a), x(b)
On peut faire la formule de Rieman en posant dx=(b-a)/N
et en sommant l'infinité de petits rectangles....
Cependant, si x est continue croissante sur [a,b]
soit dt=b-a/N
[x(a],x(b)]=union disjointe de n=0 à N-1 des [x(a+ndt), x(a+(n+1)dt)]
La largeur de ces intervalles est dx(a+ndt)
Pour trouver l'aire sous la courbe, on peut donc sommer l'aire des rectangles de largeur dx(a+ndt) et de hauteur f(x(a+ndt))
D'où la formule...
C'est pas très clair je crois....
On peut faire la formule de Rieman en posant dx=(b-a)/N
et en sommant l'infinité de petits rectangles....
Cependant, si x est continue croissante sur [a,b]
soit dt=b-a/N
[x(a],x(b)]=union disjointe de n=0 à N-1 des [x(a+ndt), x(a+(n+1)dt)]
La largeur de ces intervalles est dx(a+ndt)
Pour trouver l'aire sous la courbe, on peut donc sommer l'aire des rectangles de largeur dx(a+ndt) et de hauteur f(x(a+ndt))
D'où la formule...
C'est pas très clair je crois....
j'ajoute que par la méthode du changement d'intervalle de l'intégrale, on peut trouver la formule du périmètre d'un cercle pour ceux que ca intéresse ....
Seul prérequis :
*Longueur d'un arc de courbe :]^2)\, dx)
*périmètre d'un cercle de rayon 1 : 2pi
Et puis en fait, on démontre finalement les homotéties par le changement de variable .... non ?
Seul prérequis :
*Longueur d'un arc de courbe :
*périmètre d'un cercle de rayon 1 : 2pi
Et puis en fait, on démontre finalement les homotéties par le changement de variable .... non ?
duchere a écrit:Ce qui me prait sympa avec cette formule générale, c'est que toute fonction y continue croissante sur a,b telle que y(a)=x(a) et y(b)=x(b) peut prendre la place de la fonction x ....
Il faut des conditions un poil plus fortes que ca : y doit être un C1-difféomorphisme, c'est à dire une application bijective et continûment différentiable et dont la réciproque est aussi continûment différentiable...
si je ne m'abuse...
nox, je n'en sais rien... J'ai aucune connaissance....
et, dx(a+n (b-a)/N) n'est qu'une notation, j'ai même pas besoin de mettre ca....
Puisque lorsque je l'utilise après, je mets en dénominateur (b-a)/N et en déduit que c'est la dérivée car x est croissante donc c'est lim f(x+h)-f(x) / h
Non ?
Jean
et, dx(a+n (b-a)/N) n'est qu'une notation, j'ai même pas besoin de mettre ca....
Puisque lorsque je l'utilise après, je mets en dénominateur (b-a)/N et en déduit que c'est la dérivée car x est croissante donc c'est lim f(x+h)-f(x) / h
Non ?
Jean
Mais je ne comprends pas trop le but en fait...
Ca partait sur le pas variable et ca va sur le changement de variable.
Si j'ai bien compris tu veux faire varier le pas en changeant la variable et au lieu de prendre la subdivision tu prends l'image de la subdivision par l'application du changement de variable c'est ca?
Mais le pas variable n'a aucun intérêt si il ne dépend pas de la fonction intégrée. Les méthode à pas variable sont robustes et plus efficaces que les méthodes à pas fixe justement pour cette raison (cf Runge Kutta par exemple...the very best of... http://fr.wikipedia.org/wiki/M%C3%A9thodes_de_Runge-Kutta mais bon là c'est plutôt de l'analyse numérique).
Ca partait sur le pas variable et ca va sur le changement de variable.
Si j'ai bien compris tu veux faire varier le pas en changeant la variable et au lieu de prendre la subdivision tu prends l'image de la subdivision par l'application du changement de variable c'est ca?
Mais le pas variable n'a aucun intérêt si il ne dépend pas de la fonction intégrée. Les méthode à pas variable sont robustes et plus efficaces que les méthodes à pas fixe justement pour cette raison (cf Runge Kutta par exemple...the very best of... http://fr.wikipedia.org/wiki/M%C3%A9thodes_de_Runge-Kutta mais bon là c'est plutôt de l'analyse numérique).
Oui non en fait, le but n'était pas le pas variable....
Le but était d'établir un cheminement pour obtenir le changement de variable...
Disons qu'on veut l'intégrale de i à j de f(x)
si x est continue croissante sur [a,b] avec x(a)=i et x(b)=j, on peut exprimer l'intégrale, mais avec un pas variable....
Pour obtenir une intégarle avec pas non variable, on fait apparaitre la dérivée.... Et on obtient la formule du changement de variable
Voilà c'est tout.
Jean
Le but était d'établir un cheminement pour obtenir le changement de variable...
Disons qu'on veut l'intégrale de i à j de f(x)
si x est continue croissante sur [a,b] avec x(a)=i et x(b)=j, on peut exprimer l'intégrale, mais avec un pas variable....
Pour obtenir une intégarle avec pas non variable, on fait apparaitre la dérivée.... Et on obtient la formule du changement de variable
Voilà c'est tout.
Jean
Beh le nouvel espace est le même puisque x(a)=i et x(b)=j, si ju subdivise [x(a),x(b)], ca ne sert à rien....
Ce que je fais, c'est que plutot que de faire varier x linérairement (x(t)=t), je le fais varier comme entre x(a)=i et x(b)=j, mais alors, il varie comme sa fonction associée....
Par exemple, si j'intègre sur [0,1]
Que je vois dans f(x) que si x était un sinus ce qui est possible car on sin prend des valeurs sur [0,1], cela arrangerait les calculs, eh bien, je fais apparaitre le sinus....
Cependant, x ne varie plus comme x(t)=t mais comme x(t)=sin t
Donc le pas n'est plus constant....
Non ?
Jean
Ce que je fais, c'est que plutot que de faire varier x linérairement (x(t)=t), je le fais varier comme entre x(a)=i et x(b)=j, mais alors, il varie comme sa fonction associée....
Par exemple, si j'intègre sur [0,1]
Que je vois dans f(x) que si x était un sinus ce qui est possible car on sin prend des valeurs sur [0,1], cela arrangerait les calculs, eh bien, je fais apparaitre le sinus....
Cependant, x ne varie plus comme x(t)=t mais comme x(t)=sin t
Donc le pas n'est plus constant....
Non ?
Jean
42 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
