Intégration

[pffffffffff]

Bonjour,
J'ai besoin d'aide pour intégrer la fonction suivante :
sin(u) cos²(u)

[capitaine nuggets]

Salut !

Utilise le fait qu'une primitive de la fonction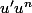 est la fonction .

[pffffffffff]

Ok merci beaucoup !

ça semble marcher

[pffffffffff]

Re bonsoir,

En fait, mon problème est le suivant :

Pour tout entier naturel n, on pose

1. a. Montrer que
b. Calculer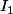

2. a. Justifier soigneusement que pour tout n appartenant à N,
b. Etudier les variations de la suite , n appartenant à N. Que peut-on en déduire ?

Pour la 1.a j'utilise le changement de variable x = sin u
Pour la 1. b je trouve 1/3 (sans grande conviction)
Pour la 2. a je suis parti sur une démo par récurrence grâce à l'initialisation faite dans la 1.a mais après je bloque sur l'hérédité..

Merci d'avance

[Pseuda]

Bonsoir,

Pour la 2b, au vu de la question, il me semble qu'il est seulement demandé d'étudier la limite de la suite In. Dans tous les cas, si tu veux faire une démonstration par récurrence, il faudrait déjà avoir une formule.

[pffffffffff]

Pour la 2b, vous ne pensez pas qu'il y ait besoin de dériver et trouver le signe de cette dérivée pour trouver les variations ?
Sinon pour la 2a je pensais partir des deux premières questions et généraliser pour tout n mais je n'arrive pas à poser ça de façon mathématiques.

[infernaleur]

Salut,
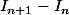Rappel (positivité de l'intégrale) :
Soit f une fonction continue sur un intervalle
(1) Si f est positive sur [a,b] alors
(2) Si f est négative sur [a,b] alors

Donc pour la 2)a) tu peux en déduire directement de ce qui précède que: .
Ensuite le point subtile a montrer est que l’inégalité est en fait stricte (donc ).
Pour cela tu peux utiliser cette propriété (connue ?) :

Propriété :
Soit f une fonction continue sur un intervalle et qui est de signe constant sur [a,b].
Si , Alors


Ensuite pour la dernière question, on te demande les variations d'une suite pas d'une fonction, donc je pense que dériver n'est pas la première chose a laquelle tu dois penser. Pourquoi ne pas tout simplement employer la méthode habituelle ? C'est-à-dire étudier le signe de .

[aviateur]

Pour la 1. b je trouve 1/3 (sans grande conviction)

Je viens de vérifier, il me semble que c'est correct.
Pourquoi sans grande conviction? Tu ferais bien d'expliquer même un peu rapidement comment tu as fait ou bien dire pourquoi tu n'es pas très convaincu de ton calcul.

[pffffffffff]

Je me suis trompé à plusieurs sur ce calcul et à chaque fois les résultats que je trouvais étaient plausibles mais maintenant je peux confirmer ce résultat avec les questions qui suivent.
Merci d'avoir vérifier quand même !

[pffffffffff]

Merci beaucoup infernaleur, je ne connaissais pas la propriété !

[pffffffffff]

La suite de mon exercice est la suivante :

3. Soit n un entier naturel non nul. A l'aide dune intégration par parties, montrer que :



En déduire que pour tout n appartenant à N*,

J'ai fais l'integration par partie de In+1 mais je trouve :
Il ya certainement une erreur de calcule mais je ne vois pas laquelle..

[aviateur]

Si tu ne mets pas ton calcul on ne peut pas voir où es ton erreur!

[pascal16]

quand tu dérives x^n, tu as n.x^(n-1), c'est n en facteur, pas n+1

[pffffffffff]

pascal 16, j'ai intégré In+1 par partie et non In..

J'ai posé :
d'ou
d'ou

puis :

[aviateur]

Rebonjour
v n'est pas correct. D'ailleurs pour t'en assurer, dérive v et tu ne trouveras pas ton v'.
D'ailleurs je te déconseille de faire comme cela car une primitive de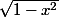 ne va pas te donner la forme escomptée.
Sinon regarde le conseil de @pascal16 ou alors (c'est que j'aurai fait):
tu pars de l'intégrale qui te donne la nouvelle expression de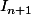 (c'est à dire l'intégrale avec la puissance 3/2. ) Et là tu fais ton ipp "la dérivée avec la puissance 3/2" va te donner du ""
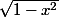J'ai pas fait le calcul bien sûr mais c'est certain que ça va marcher.

[pffffffffff]

Dans ce cas je devrais intégrer In+1 par partie.

[pascal16]

tu intègres x*sqrt(1-x²) car c'est une forme u'*sqrt(u)

ta dérivée de v n'est pas bonne, c'est une forme "u/v" de dérivée compliquée

[pffffffffff]

ok merci beaucoup !
ahhhhh mais oui bien sur, c'est pour ça que tu me disais ça dans ton message...

[pffffffffff]

Donc :
d'ou
d'ou

puis :

[pascal16]

là c bon