Injectivité des morphismes de groupe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par PythagoreSauvage » 30 Nov 2021, 10:35
par PythagoreSauvage » 30 Nov 2021, 10:35
Bonjour à tous ! Je me posais une question la dernière fois, pourquoi un morphisme de groupes n'est pas forcément injectif ? Pour moi il l'est tout le temps, j'ai essayé de faire une preuve rigoureuse :
Soient
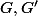
deux groupes.
Soient
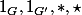
respectivement les éléments neutres et les lois de composition internes de
Soit
 \end{array} \right. \text{un morphisme de groupes})
c'est à dire que

est telle que pour tous
 = f(x) \star f(y))
On a aussi que :
 = 1_{G'} \\ f(x^{-1}) = f^{-1}(x) \text{ pour tout } x \in G)
Considérons
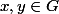
tels que
 = f(y))
et montrons qu'alors

. On a :
 \star [f(y)]^{-1} = f(y) \star [f(y)]^{-1} \text{ en composant \`{a} droite par } [f(y)] ^{-1} \text{ qui existe car tous les \'{e}l\'{e}ments de } G', \text{ donc en particulier } f(y), \text{ sont inversibles par d\'{e}finition d'un groupe})
Ainsi,
 \star [f(y)]^{-1} = 1_{G'} \\ f(x) \star f(y^{-1}) = 1_{G'} \\ f(x \ast y^{-1}) = 1_{G'} \text{ car } f \text{ est un morphisme de groupes} \\ x \ast y^{-1} = 1_{G} \\x = y)
Et on a le résultat.. Pouvez vous me dire pourquoi mon raisonnement est faux (car a priori les morphismes de groupes ne sont pas tous forcément injectifs..) s'il vous plaît ? Bonne journée et merci
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 30 Nov 2021, 11:50
par tournesol » 30 Nov 2021, 11:50
de
=1_{G'})
tu déduis
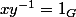
Tu suppose que ker(f)=1G , ce qui caractérise l'injectivité des morphismes de groupe , mais qui est faux en général .
=1_{G'})
définit un morphisme de groupes ...non injectif .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 30 Nov 2021, 12:09
par tournesol » 30 Nov 2021, 12:09
Remarque sur les morphismes de groupe : injectif pour UN
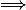
injectif pour TOUS
Supposons qu'il existe a dans G et b dans G' tels que: f(a)=b et
=b)\implies(x=a))
Alors le morphisme f est injectif .
supposons f(x)=f(y)
Alors
=f(x)(f(y))^{-1}f(a)=f(x)(f(x))^{-1}b=1_{G'}b=b)
Donc
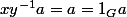
; donc par régularité
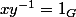
Donc x=y
Autant alors caractériser cette propriété avec "l'injectivité par rapport à
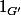
:
f(x)=1G'
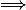
x=1G (étant entendu que f(1G)=1G', 1G joue le rôle de a et 1G' celui de b)
C'est à dire ker(f)={1G}
Les morphismes étendent souvent des propriétés ponctuelles a tous les éléments .
Pa exemple une application linéaire est continue ssi elle l'est en un point donné .
 par PythagoreSauvage » 30 Nov 2021, 15:15
par PythagoreSauvage » 30 Nov 2021, 15:15
tournesol a écrit:de
=1_{G'})
tu déduis
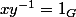
Tu suppose que ker(f)=1G , ce qui caractérise l'injectivité des morphismes de groupe , mais qui est faux en général .
=1_{G'})
définit un morphisme de groupes ...non injectif .
Ah oui !! En effet là est l'erreur. En somme je prouve quelque chose en supposant que c'est vrai, pas mal.. Et merci pour vos réponses

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
