Fonctions développables de séries entières
18 messages
- Page 1 sur 1
Fonctions développables de séries entières
Bonjour je n'arrive pas à résoudre cet exercice pouvez-vous m'aider? svp
Merci
f(x)= exp (-1/x²) si x différent de 0
f(x)=0 si x=0
1) Montrer que f est C infini sur R et f^n(x)=Pn (1/x) exp(-1/x²) si x différent de 0 avec Pn un polynôme.
2)Montrer que f^n(0)=0 quelque soit n.
3) Montrer que f n'est égale à la somme de la série de Taylor sur aucun intervalle ]-R,R[ avec R>0.
Pour la première question j'ai mis que f est C infini sur R car -/x² est C infini sur R et exp (x) aussi. Mais je ne sais pas si c'est juste et si cela suffit pour dire que f est C infini sur R. Ensuite j'ai calculé f'(x) j'ai trouvé f'(x)= 2/x² (1/x) exp(-1/x²)=P1 (1/x) exp(-1/x²). Puis j'ai fait une récurrence mais je ne sais pas si elle est correcte. f^(n+1) (x)= Pn (1/x)exp(-1/x²) + P1 (1/x)exp(-1/x²)=(1/x)exp(-1/x²)(Pn+P1)= Pn+1 (1/x)exp(-1/x²).
Puis j'ai mis donc on a bien f^n(x)=Pn (1/x)exp(-1/x²).
Est-ce que c'est correcte?
Pour la deuxième question j'ai dit que f^n(x)=0 car f(0)=0.
Et la troisième question je ne sais pas du tout comment faire.
Merci
f(x)= exp (-1/x²) si x différent de 0
f(x)=0 si x=0
1) Montrer que f est C infini sur R et f^n(x)=Pn (1/x) exp(-1/x²) si x différent de 0 avec Pn un polynôme.
2)Montrer que f^n(0)=0 quelque soit n.
3) Montrer que f n'est égale à la somme de la série de Taylor sur aucun intervalle ]-R,R[ avec R>0.
Pour la première question j'ai mis que f est C infini sur R car -/x² est C infini sur R et exp (x) aussi. Mais je ne sais pas si c'est juste et si cela suffit pour dire que f est C infini sur R. Ensuite j'ai calculé f'(x) j'ai trouvé f'(x)= 2/x² (1/x) exp(-1/x²)=P1 (1/x) exp(-1/x²). Puis j'ai fait une récurrence mais je ne sais pas si elle est correcte. f^(n+1) (x)= Pn (1/x)exp(-1/x²) + P1 (1/x)exp(-1/x²)=(1/x)exp(-1/x²)(Pn+P1)= Pn+1 (1/x)exp(-1/x²).
Puis j'ai mis donc on a bien f^n(x)=Pn (1/x)exp(-1/x²).
Est-ce que c'est correcte?
Pour la deuxième question j'ai dit que f^n(x)=0 car f(0)=0.
Et la troisième question je ne sais pas du tout comment faire.
bonjour,
pour la premiere question, tu es sure que (-1/x²) est C infini sur ... R? je croyais pourtant que (-1/x²) n'était pas définit en zéro...
en fait c'est presque ca:
donc f C infini sur R
question 2
il faut remarquer la nuance: f(n)(x)=0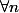 non parce que f(x)=0
non parce que f(x)=0
mais parce que f est définit en 0 par f(0)=0, donc en dérivant f en zero, on a f'(0)=(0)'=0, et de meme f''(0)=0, etc...
pour la premiere question, tu es sure que (-1/x²) est C infini sur ... R? je croyais pourtant que (-1/x²) n'était pas définit en zéro...
en fait c'est presque ca:
- (-1/x²) est C infini sur R\{0} (car fraction de polynome dont le dénominateur s'annule en x=0)
- exp: R->R est C infini
- f est continu en 0 car
donc f C infini sur R
question 2
il faut remarquer la nuance: f(n)(x)=0
mais parce que f est définit en 0 par f(0)=0, donc en dérivant f en zero, on a f'(0)=(0)'=0, et de meme f''(0)=0, etc...
bonjour
je me souviens avoir répondu exactement à la même question ici il y a quelque temps.
cf bauzau la continuité de f en 0 n'assure en rien que f est de classe c infinie en 0
f est c infinie sur R*
et pour x >0 f^(n) (x) = Pn(x) /x^(3n) f(x) avec Pn polynôme ( récurrence sur n)
on montre ainsi qu' en 0 lim f^(n) = 0 ce qui garantit que f est C infinie en 0 avec dérivées toutes nulles
2) la série de taylor est donc identiquement nulle ce que f n 'est pas sur tout intervalle ]-r,r[ r>0
je me souviens avoir répondu exactement à la même question ici il y a quelque temps.
cf bauzau la continuité de f en 0 n'assure en rien que f est de classe c infinie en 0
f est c infinie sur R*
et pour x >0 f^(n) (x) = Pn(x) /x^(3n) f(x) avec Pn polynôme ( récurrence sur n)
on montre ainsi qu' en 0 lim f^(n) = 0 ce qui garantit que f est C infinie en 0 avec dérivées toutes nulles
2) la série de taylor est donc identiquement nulle ce que f n 'est pas sur tout intervalle ]-r,r[ r>0
je n'avais pas lu la question 1) qui demande f^(n) (x) = Pn(1/x) f(x)
pour l'expression que je proposais (juste également)
n= 0 ok avec P0 = 1
on suppose le résultat pour n on a
pour x>0 f^(n) (x) = Pn(x) /x^(3n) f(x)
d'où
f^(n+1) (x) = P ' n (x) /x^(3n) f(x) - 3nPn(x) /x^(3n+1) f(x) +2Pn(x)/x^(3n+3) f(x) en dérivant comme un produit de trois facteurs = [x^3 P'n(x) -3nx^2Pn(x) +2Pn(x) ]/x^(3n+3) f(x)
et le résultat pour n+1
pour l'expression que je proposais (juste également)
n= 0 ok avec P0 = 1
on suppose le résultat pour n on a
pour x>0 f^(n) (x) = Pn(x) /x^(3n) f(x)
d'où
f^(n+1) (x) = P ' n (x) /x^(3n) f(x) - 3nPn(x) /x^(3n+1) f(x) +2Pn(x)/x^(3n+3) f(x) en dérivant comme un produit de trois facteurs = [x^3 P'n(x) -3nx^2Pn(x) +2Pn(x) ]/x^(3n+3) f(x)
et le résultat pour n+1
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
