Fausse implication
23 messages
- Page 1 sur 2 - 1, 2
Fausse implication
Si P=>non(P)
Alors [non(P) OU non(P)]=non(P).
La table de vérité des deux ensemble n'est pas la même
Absurde
Mais en exhibant le négation de P=>non(P)
On a P et non(P)=ensemble vide
Absurde
Donc ni l'affirmation ni la négation ni ne veulent dire quelque chose.
P=>non(P)
Est ce une implication ?
Alors [non(P) OU non(P)]=non(P).
La table de vérité des deux ensemble n'est pas la même
Absurde
Mais en exhibant le négation de P=>non(P)
On a P et non(P)=ensemble vide
Absurde
Donc ni l'affirmation ni la négation ni ne veulent dire quelque chose.
P=>non(P)
Est ce une implication ?
Re: Fausse implication
Bonsoir,
( A=>B) <=> (non(A) ou B)
P => non(P)
cette implication se traduit par
non(P) ou non(P)
d'où
non(P) (sous-entendu vraie)
Donc P est fausse.
( A=>B) <=> (non(A) ou B)
P => non(P)
cette implication se traduit par
non(P) ou non(P)
d'où
non(P) (sous-entendu vraie)
Donc P est fausse.
Modifié en dernier par mathelot le 08 Avr 2022, 21:11, modifié 1 fois.
Re: Fausse implication
Surveillance a écrit:Mais en exhibant la négation de P=>non(P)
On a P et P
P et P = P
P est vraie
car non( A =>B) <=> (A et non(B))
Re: Fausse implication
Bonjour,
Il ne s'agit pas d'ensembles mais de propositions. Et la table de vérité de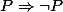 est bien la même que celle de
est bien la même que celle de 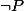 . Que vois-tu comme différence ?
. Que vois-tu comme différence ?
La table de vérité des deux ensemble n'est pas la même
Il ne s'agit pas d'ensembles mais de propositions. Et la table de vérité de
Re: Fausse implication
Qu'est ce qui ne va pas ?
Non (P) vraie donc P faux
Ma maladie implique de nier ma maladie
Non (P) vraie donc P faux
Ma maladie implique de nier ma maladie
Re: Fausse implication
Joli! Il faut être dans le déni ou dans l'absurde pour rendre vraie une proposition du type P=>non P .
C'est là tout le charme du surréalisme ...
C'est là tout le charme du surréalisme ...
Re: Fausse implication
Ici on est censé faire du calcul propositionnel. 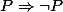 est logiquement équivalent à
est logiquement équivalent à 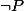 et est donc faux quand
et est donc faux quand  est vrai et vrai quand
est vrai et vrai quand  est faux.
est faux.
Surveillance, j'ai l'impression que tu veux jouer à autre chose. Mais à quoi ,
Surveillance, j'ai l'impression que tu veux jouer à autre chose. Mais à quoi ,
Re: Fausse implication
Ma maladie : Vrai Faux
Nier ma maladie : Faux Vrai
La table de vérité de nier ma maladie est-elle exacte ?
Nier ma maladie est non(P) ?
Nier ma maladie : Faux Vrai
La table de vérité de nier ma maladie est-elle exacte ?
Nier ma maladie est non(P) ?
Re: Fausse implication
Prendre des phrases de la vie courante comme propositions du calcul des propositions est sujet à contresens.
Par exemple, la négation de "X est malade" n'est certainement pas "X nie être malade", mais tout simplement "X n'est pas malade". En effet, X peut très bien en même temps être malade et nier être malade.
Et quand on traduit le du calcul propositionnel par le "Si ... alors ..." du langage courant, on introduit une notion de causalité qui n'existe absolument pas dans le calcul propositionnel. Le
du calcul propositionnel par le "Si ... alors ..." du langage courant, on introduit une notion de causalité qui n'existe absolument pas dans le calcul propositionnel. Le  du calcul propositionnel est un connecteur logique qui fabrique une nouvelle proposition à partir de deux propositions.
du calcul propositionnel est un connecteur logique qui fabrique une nouvelle proposition à partir de deux propositions.
Par exemple, la négation de "X est malade" n'est certainement pas "X nie être malade", mais tout simplement "X n'est pas malade". En effet, X peut très bien en même temps être malade et nier être malade.
Et quand on traduit le
Re: Fausse implication
Pour enfoncer le clou "ma maladie" n'est pas, ne peut pas être vu comme, une proposition ayant une valeur de vérité. dire que "ma maladie" est vraie ou que "ma maladie" est faux n'a pas de sens.
A la rigueur on peut dire que
- "l'individu X est malade à l'instant t" est une affirmation (vraie ou fausse) dont la négation est "l'individu X n'est pas malade à l'instant t"
- "je suis atteint de la maladie Y" est une affirmation (vraie ou fausse) dont la négation est "je ne suis pas atteint de la maladie y"
Le fait que (A => B) soit vraie si A est faux déroute de nombreux néophytes. Je trouve que l'explication qui marche le mieux est la suivante.
Si on sait que (A => B) est vraie et on sait que B est vraie on ne peut rien dire sur A !
Exemple :
A: " X est un chat"
B: "X est mortel"
Affirmation vraie : "tous les chats sont mortels", donc (A=>B) est vraie.
Seconde affirmation vraie : "Socrate est mortel", donc B est vraie (pour X = Socrate).
J'ai (A=>B) vraie, et B vraie, si je regarde la table je vois que je ne sais pas dire si A est vraie (Socrate est un chat) ou fausse (Socrate n'est pas un chat).
C'est ce qui fait toute la différence entre (A => B) et (A<=>B).
P.S: pour les trolls qui prétendent que la logique ne sert à rien : toute démonstration mathématique s'appuie sur ces règles logiques, ou plutôt sur les diverses méthodes de démonstrations qui en découlent et dont la validité a été démontrée (démonstration par absurde, par recurrence, par analyse synthèse...).
A la rigueur on peut dire que
- "l'individu X est malade à l'instant t" est une affirmation (vraie ou fausse) dont la négation est "l'individu X n'est pas malade à l'instant t"
- "je suis atteint de la maladie Y" est une affirmation (vraie ou fausse) dont la négation est "je ne suis pas atteint de la maladie y"
Le fait que (A => B) soit vraie si A est faux déroute de nombreux néophytes. Je trouve que l'explication qui marche le mieux est la suivante.
Si on sait que (A => B) est vraie et on sait que B est vraie on ne peut rien dire sur A !
Exemple :
A: " X est un chat"
B: "X est mortel"
Affirmation vraie : "tous les chats sont mortels", donc (A=>B) est vraie.
Seconde affirmation vraie : "Socrate est mortel", donc B est vraie (pour X = Socrate).
J'ai (A=>B) vraie, et B vraie, si je regarde la table je vois que je ne sais pas dire si A est vraie (Socrate est un chat) ou fausse (Socrate n'est pas un chat).
C'est ce qui fait toute la différence entre (A => B) et (A<=>B).
P.S: pour les trolls qui prétendent que la logique ne sert à rien : toute démonstration mathématique s'appuie sur ces règles logiques, ou plutôt sur les diverses méthodes de démonstrations qui en découlent et dont la validité a été démontrée (démonstration par absurde, par recurrence, par analyse synthèse...).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Fausse implication
Merci pour vos réponses.
Ne peut on pas faire une fonction Négation qui à tout élément de ma maladie nie ma maladie. Cette fonction seraitvà valeur dans A
Avec A les gens pas malade
Ne peut on pas faire une fonction Négation qui à tout élément de ma maladie nie ma maladie. Cette fonction seraitvà valeur dans A
Avec A les gens pas malade
Re: Fausse implication
Ne peut on pas faire une fonction Négation qui à tout élément de ma maladie nie ma maladie. Cette fonction seraitvà valeur dans A
Avec A les gens pas malade
Cette phrase n'a pas de sens.
Qu'est ce que "ma maladie" ? [On dirait un ensemble puisque tu dis "à tout élément de ma maladie"
Que veut dire "nie ma maladie" ?
Si ta fonction est à valeur dans "les gens pas malade" cela veut dire que quand tu "nie ma maladie" sur un élément de "ma maladie" tu obtiens un "gens pas malade"...
Bref. Sans queue ni tête.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Fausse implication
M les malades et A les pas malades .
Je vois ta négation de M vers P(A)
Au malade m je fais correspondre l'ensemble des pas malades qui nient la maladie de m .
Cet ensemble de personne éventuellement vide est appelé négation de m ou non m .
Signé TouRnesOL avec un seul L
Je vois ta négation de M vers P(A)
Au malade m je fais correspondre l'ensemble des pas malades qui nient la maladie de m .
Cet ensemble de personne éventuellement vide est appelé négation de m ou non m .
Signé TouRnesOL avec un seul L
Re: Fausse implication
Sylviel a écrit:Le fait que (A => B) soit vraie si A est faux déroute de nombreux néophytes. Je trouve que l'explication qui marche le mieux est la suivante.
Je pense que le plus simple est de dire que "pr tt x ( A(x)=>B(x) )" est faux uniquement quand A(x) est vrai et que B(x) est faux, donc dans les autres cas elle n'est pas fausse.
(Et pour démontrer une implication, il suffit donc de traiter uniquement les cas où A(x) est vrai)
Là où cela pose un problème de compréhension c'est lorsque A(x) n'est jamais vrai, car cela perd en sens.
(Dans ce cas puisqu'il n'y a aucun cas où A(x) est vrai, il n'y a plus rien à démontrer.
L'implication n'étant donc jamais contredite, elle sera alors considérée comme "vraie" dans le sens où il n'existe pas de contre-exemple)
Et c'est de là que la traduction par un "si A alors B" du langage courant devient problématique.
Car dans le langage courant on utilise un "si" uniquement si ce qui suit peux prendre les deux valeurs vrai et faux, au moins à priori, avec de plus un lien entre A et B. (Lorsque A est toujours vrai ou toujours faux, on n'utilise pas de "si")
Notamment tous les exemples du type "Si 1+1=3 alors il pleut des diamants sur Jupiter" n'ont pas de sens courant! (en dehors d'un effet de style ou d'un effet rhétorique) .
Donc dans le langage courant (qui n'est pas celui de la logique mathématique) on ne dira pas que cet énoncé est vrai, contrairement à la logique mathématique. C'est une des différence entre ces deux langages et qui est la source des difficultés de compréhension des néophytes comme tu dis. Peut-être que ça en aidera certains d'entre eux.
Bonne soirée.
Modifié en dernier par LuiLui le 25 Mai 2023, 17:39, modifié 1 fois.
Re: Fausse implication
Salut,
Perso, comme GaBuZoMeu, ce qui me semble être LA différence essentielle entre l'implication mathématique et les propositions conditionnelles du Français, c'est la notion de causalité : la cause précède (dans le temps) l'effet et pas le contraire. Par exemple, la contraposée du banal "Demain, s'il fait beau, j'irais faire du vélo" donne "Demain, si je ne vais pas faire de vélo, il ne fera pas beau" qui, littéralement, signifie que le locuteur est capable de faire la pluie et le beau temps.
Par contre, l'affirmation "Si 1+1=3 alors il pleut des diamants sur Jupiter", a, pour moi, un sens courant parfaitement acceptable, au même titre que les classiques "je fera ça la semaine des 4 jeudis" ou "je me marierais quand les poules auront des dents".
Enfin, à mon sens, pour comprendre ce qu'est l'implication mathématique, il suffit de savoir que la proposition) est vraie et de comprendre que ça signifie en particulier que
est vraie et de comprendre que ça signifie en particulier que ) et
et ) sont des propositions vraies.
sont des propositions vraies.
Perso, comme GaBuZoMeu, ce qui me semble être LA différence essentielle entre l'implication mathématique et les propositions conditionnelles du Français, c'est la notion de causalité : la cause précède (dans le temps) l'effet et pas le contraire. Par exemple, la contraposée du banal "Demain, s'il fait beau, j'irais faire du vélo" donne "Demain, si je ne vais pas faire de vélo, il ne fera pas beau" qui, littéralement, signifie que le locuteur est capable de faire la pluie et le beau temps.
Par contre, l'affirmation "Si 1+1=3 alors il pleut des diamants sur Jupiter", a, pour moi, un sens courant parfaitement acceptable, au même titre que les classiques "je fera ça la semaine des 4 jeudis" ou "je me marierais quand les poules auront des dents".
Enfin, à mon sens, pour comprendre ce qu'est l'implication mathématique, il suffit de savoir que la proposition
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fausse implication
Bonjour Ben, attention les exemples que tu donnes (la semaine des 4 jeudis et les poules auront des dents) sont des figures de styles que l'on appelle un adynaton il me semble, et ne sont d'ailleurs jamais formulées avec un "si alors" à cause justement du caractère invraisemblable de la phrase.
Je vais préciser à propos de la phrase sur Jupiter que quand je dis "cela n'a pas de sens" je veux dire "cela n'a pas de sens de se poser la question : cette implication est-elle vraie ? est-elle est fausse?"
Je mets de côté les effets rhétoriques et les effets de style.
Bonne journée.
Je vais préciser à propos de la phrase sur Jupiter que quand je dis "cela n'a pas de sens" je veux dire "cela n'a pas de sens de se poser la question : cette implication est-elle vraie ? est-elle est fausse?"
Je mets de côté les effets rhétoriques et les effets de style.
Bonne journée.
Modifié en dernier par LuiLui le 25 Mai 2023, 17:31, modifié 1 fois.
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
