Exponentielle d'une matrice !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 15:24
par barbu23 » 23 Jan 2009, 15:24
Bonjour :
Soit :
 $)
Comment calcule-t-on : la dérivée de l'expression suivante :
 = e^{tA} $)
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 15:26
par barbu23 » 23 Jan 2009, 15:26
Je sais que :
 = A.e^{tA} $)
, mais comment la calculer ?
Merci d'avance de votre aide !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2009, 15:49
par XENSECP » 23 Jan 2009, 15:49
Lol utilise simplement :
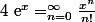
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 16:11
par barbu23 » 23 Jan 2009, 16:11
Bonjour "XENSECP'' :
Voiçi comment je procède :
La fonction :
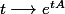
est définie sur
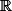
tout entier.
Soit :

On a :
A} - e^{t_{0}A}}{t} = e^{t_{0}A}. (\frac{e^{hA} - I_{n}}{h}) $)
Or :
 $)
Par conséquent :
A} - e^{t_{0}A}}{t} = \displaystyle \lim_{h \longrightarrow 0} e^{t_{0}A}. (\frac{e^{hA} - I_{n}}{h}) = \displaystyle \lim_{h \longrightarrow 0} e^{t_{0}A}. A . (I_{n}+\frac{hA}{2!}+ ... ) = A . e^{t_{0}A} $)
Par conséquent :
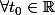
:
'(t_{0}) = A . e^{t_{0}A} $)
CQFD
C'est bien comme ça ? :happy2:
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 23 Jan 2009, 17:11
par L.A. » 23 Jan 2009, 17:11
Bonjour.
on peut utiliser un théorème de dérivation sous le signe somme :
la série des dérivées converge uniformément sur tout segment vers
t |-> Aexp(tA)
et la série converge simplement
donc la limite simple t |-> exp(tA) est C1 est sa dérivée est t |-> Aexp(tA)
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 23 Jan 2009, 17:18
par L.A. » 23 Jan 2009, 17:18
pour ce que tu proposes : il faut vérifier dans le passage à la limite final que le terme (In + hA/2!+...) tend bien vers In quand h->0.
C'est vrai car la fonction h |-> In + hA/2! + ... est somme d'une série normalement convergente sur tout segment, donc continue.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 19:47
par barbu23 » 23 Jan 2009, 19:47
Merci "L.A." pour ces précisions !
J'ai une autre question à vous poser :
Xomment montre-t-on que l'application :
 = \displaystyle \sum_{k=0}^{+\infty} \frac{A^{k}}{k!} $)
est de classe
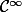
?
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 20:03
par barbu23 » 23 Jan 2009, 20:03
Re-bonsoir :
Soient :
 $)
:
On a :
-f(A) = \exp (A+H) - \exp (A) = \exp (A). \exp (H) - \exp (A) = \exp(A) ( \exp (H) - I_{n} ) = \exp (A) ( \displaystyle \sum_{k=0}^{+\infty} \frac{H^k}{k!} - I_{n} ) = \exp (A) ( \displaystyle \sum_{k=1}^{+\infty} \frac{H^k}{k!}) = \exp (A) . H . ( \displaystyle \sum_{k=1}^{+\infty} \frac{H^{k-1}}{k!}) = \exp (A) . H + \exp ( A) . ( \displaystyle \sum_{k=2}^{+\infty} \frac{H^{k-1}}{k!}) $)
On pose :
 = \exp (A) . H $)
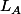
est linéaire continue, et :
-f(A)- L_{A}|| = || \exp ( A) . ( \displaystyle \sum_{k=2}^{+\infty} \frac{H^{k-1}}{k!}) || \longrightarrow 0 $)
quant
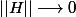
Donc :

est de classe :
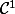
Qu'est ce qu'on fait après ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 20:43
par barbu23 » 23 Jan 2009, 20:43
SVP, aidez moi ! Merci infiniment !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 23 Jan 2009, 21:02
par Doraki » 23 Jan 2009, 21:02
Si t'as montré que exp était C1 et que sa dérivée était exp, ben t'as plus aucun calcul à faire pour montrer que exp est infiniment dérivable..
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 23 Jan 2009, 21:10
par ffpower » 23 Jan 2009, 21:10
sauf que exp(A+H)=exp(A)exp(H) n est vrai que si A et H commutent..(enfin p-e pas "que si",mais en tout cas cette relation n est pas toujours vraie)..Je crois que c est pas facile de montrer que exp est C infini
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Jan 2009, 21:13
par barbu23 » 23 Jan 2009, 21:13
Bonsoir "Doraki" :
Le problème est que je ne trouve pas :
 $)
pour la dérivée de
 $)
mais
.H $)
... ! donc, ce n'est pas la même chose que :
 $)
.. :doh:


-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 23 Jan 2009, 22:35
par nuage » 23 Jan 2009, 22:35
Salut,
la dérivée (si elle existe) d'une application de

dans

est une application de

dans l'ensemble
)
des applications linéaires de

dans

.
Si

n'est pas de dimension 1 la fonction et sa dérivée ne sont pas dans le même espace.
Ce qui explique, entre autre, que la dérivée de
)
n'est pas
)
quand
)
.
Le calcul est assez compliqué si mes souvenirs sont bons.
N'oublie pas de tenir compte de la remarque de
ffpower : on peut avoir
\neq \exp(A)\cdot \exp(H))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités