Exponentielle d'une matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 26 Avr 2015, 11:06
par marawita1 » 26 Avr 2015, 11:06
Bonjour,
J'ai un système différentiel d'ordre 1: X'(t)= A X(t) avec A est une matrice réelle d'ordre 3.
J'ai montré que A n'est pas diagonalisable mais elle est trigonalisable. J'ai pu déterminer les solutions de mon système.
Après, la question est de déduire
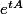
? Que dois-je faire?
Je sais que les solutions sont données par:
= e^{tA}X(0))
, mais je n'arrive pas à déterminer
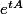
.
Merci d'avance.
-
mathelot
 par mathelot » 26 Avr 2015, 11:11
par mathelot » 26 Avr 2015, 11:11
bonjour,
on peut trouver une matrice P telle que
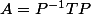
où T est trigonalisée
 P)
où D est diagonale et N nilpotente
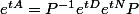

est diagonale avec des exponentielles de vp sur la diagonale
la série exponentielle

est simplement un polynome en N (une somme finie)
de degré au plus 3, puisque à partir d'un certain rang
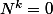
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 26 Avr 2015, 11:15
par marawita1 » 26 Avr 2015, 11:15
mathelot a écrit:bonjour,
on peut trouver une matrice P telle que
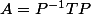
où T est trigonalisée
 P)
où D est diagonale et N nilpotente
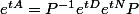
Merci pour votre réponse, oui je connais cette méthode, mais la question ici est de déduire
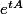
à partir des solutions X(t).
-
mathelot
 par mathelot » 26 Avr 2015, 12:56
par mathelot » 26 Avr 2015, 12:56
......................
-
mathelot
 par mathelot » 26 Avr 2015, 14:24
par mathelot » 26 Avr 2015, 14:24
Que vaut X(t) ?
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 26 Avr 2015, 15:39
par marawita1 » 26 Avr 2015, 15:39
mathelot a écrit:Que vaut X(t) ?
=\begin{pmatrix} <br />2c_1 e^{t}+ 2c_2e^{2t}-2c_3 e^{2t} +4c_3 t e^{2t} \\<br /><br />c_2 e^{2t} +2c_3 t e^{2t}\\<br /><br />c_1 e^{t} +c_2 e^{2t} +2c_3 t e^{2t}<br /> <br />\end{pmatrix})
avec

sont des constantes réelles.
-
mathelot
 par mathelot » 26 Avr 2015, 15:56
par mathelot » 26 Avr 2015, 15:56
marawita1 a écrit:=\begin{pmatrix} <br />2c_1 e^{t}+ 2c_2e^{2t}-2c_3 e^{2t} +4c_3 t e^{2t} \\<br /><br />c_2 e^{2t} +2c_3 t e^{2t}\\<br /><br />c_1 e^{t} +c_2 e^{2t} +2c_3 t e^{2t}<br /> <br />\end{pmatrix})
avec

sont des constantes réelles.
j'ai regardé sur un exemple à moi que j'ai bricolé.
j'ai démarré,non pas avec A, mais avec une matrice T trigonalisée , triangulaire supérieure.
Il s'agit d'exprimer

en fonction de
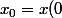;y_0;z_0)
si
=(a_1x_0+b_1y_0+c_1z_0) e^{t}+ (a_2x_0+b_2y_0+c_2z_0) e^{2t}+(a_3x_0+b_3y_0+c_3z_0) t e^{2t})
par exemple,
on réarrange la somme de manière à lire des combinaisons linéaires
de x0;y0;z0 , ce qui fera apparaître le produit matriciel de
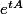
par
)
-
mathelot
 par mathelot » 26 Avr 2015, 16:11
par mathelot » 26 Avr 2015, 16:11
Si
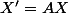
et
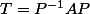
on pose
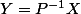
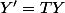
(1)
(1) s'intègre bien car T est triangulaire.
le souci réside dans les conditions initiales
vû que
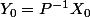
2°)
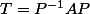
entraine
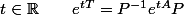
-
mathelot
 par mathelot » 26 Avr 2015, 16:28
par mathelot » 26 Avr 2015, 16:28
pour résumer:
on a le système
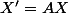
on triangule A en T
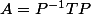
on change d'inconnue
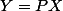
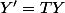 (1)
(1)
on résout (1) avec conditions initiales
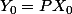
ça nous donne

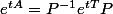
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 26 Avr 2015, 16:39
par jlb » 26 Avr 2015, 16:39
mathelot a écrit:bonjour,
on peut trouver une matrice P telle que
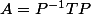
où T est trigonalisée
 P)
où D est diagonale et N nilpotente
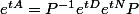

est diagonale avec des exponentielles de vp sur la diagonale
la série exponentielle

est simplement un polynome en N (une somme finie)
de degré au plus 3, puisque à partir d'un certain rang
Salut, avec D et N qui commutent, non??
-
mathelot
 par mathelot » 26 Avr 2015, 16:42
par mathelot » 26 Avr 2015, 16:42
jlb a écrit:Salut, avec D et N qui commutent, non??
oui.
@marawita: tu pourrais indiquer A ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 26 Avr 2015, 18:59
par Skullkid » 26 Avr 2015, 18:59
Bonjour, tu peux calculer
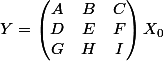
et trouver les 9 inconnues A à I (qui dépendent de t) en résolvant Y = X(t) par identification.
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 26 Avr 2015, 20:26
par marawita1 » 26 Avr 2015, 20:26
mathelot a écrit:oui.
@marawita: tu pourrais indiquer A ?
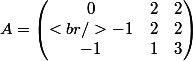

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Avr 2015, 04:25
par Ben314 » 27 Avr 2015, 04:25
Salut,
Normalement, avec ça
marawita1 a écrit:Je sais que les solutions sont données par:
= e^{tA}X(0))
et ça
marawita1 a écrit:=\begin{pmatrix} <br />2c_1 e^{t}+ 2c_2e^{2t}-2c_3 e^{2t} +4c_3 t e^{2t} \\<br />c_2 e^{2t} +2c_3 t e^{2t}\\<br />c_1 e^{t} +c_2 e^{2t} +2c_3 t e^{2t}<br />\end{pmatrix})
avec

sont des constantes réelles.
(en supposant que tu ne t'est pas gouré dans les calculs), ben tu as (quasi) fini : tu as obtenu que les solutions sont de la forme
=M(t)\begin{pmatrix}c_1\\ c_2 \\c_3 \end{pmatrix}\)
où
=\begin{pmatrix} <br />2e^{t} & \ 2e^{2t} & \ (4t-2)e^{2t} \\<br /> 0 & \ e^{2t} & \ 2t e^{2t} \\<br /> e^{t}& \ e^{2t} & \ 2 t e^{2t} \end{pmatrix})
Donc
=M(0)\begin{pmatrix}c_1\\ c_2 \\c_3 \end{pmatrix}\)
c'est à dire
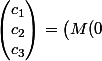\big)^{-1}X(0))
et donc
=M(t)\big(M(0)\big)^{-1}X(0))
ce qui signifie que
=M(t)\big(M(0)\big)^{-1})
Le seul calcul qu'il te reste à faire c'est celui de l'inverse de
=\begin{pmatrix} <br /> 2 & 2 & -2 \\<br /> 0 & 1 & 0 \\<br /> 1 & 1 & 0 \end{pmatrix})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 27 Avr 2015, 07:45
par mathelot » 27 Avr 2015, 07:45
marawita1 a écrit: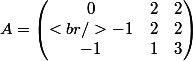
Le polynome caractéristique possède deux racines évidentes
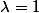
et
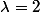
=-(\lambda-1)(\lambda-2)^2)
vecteurs propres pour
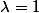
(resp.
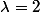
)
-
mathelot
 par mathelot » 27 Avr 2015, 08:10
par mathelot » 27 Avr 2015, 08:10
me rappelle plus comment choisir le 3ème vecteur de base, le plus judicieusement....
de manière à avoir
P)
avec

diagonale et

nilpotente qui commutent
ça s'appelle une décomposition de Dunford de l'endomorphisme u (de matrice A) dans le cas où le polynôme caractéristique est scindé.
-
mathelot
 par mathelot » 27 Avr 2015, 09:56
par mathelot » 27 Avr 2015, 09:56
mathelot a écrit:Le polynome caractéristique possède deux racines évidentes
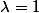
et
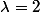
=-(\lambda-1)(\lambda-2)^2)
vecteurs propres pour
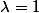
(resp.
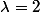
)
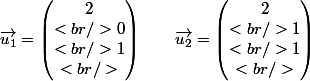
on complète par un vecteur

dans le noyau de
^2)
qui n'est pas injective
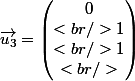
Dans la base
)
l'endomorphisme a pour matrice
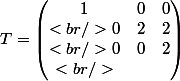
avec T=D+N , D et N commutent
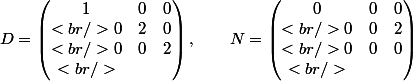
-
mathelot
 par mathelot » 27 Avr 2015, 10:33
par mathelot » 27 Avr 2015, 10:33
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 27 Avr 2015, 11:35
par marawita1 » 27 Avr 2015, 11:35
@mathelot: merci beaucoup pour vos explications.
@Ben314: merci bien, c'est génial.
-
mathelot
 par mathelot » 27 Avr 2015, 14:43
par mathelot » 27 Avr 2015, 14:43
re,
d'après
(1)e^{2t} && 2 e^{2t}-2e^{t} && (4t-2)e^{2t}+2e^{t} \\<br />-te^{2t} && e^{2t} && 2te^{2t} \\<br />-te^{2t} && e^{2t} - e^{t} && 2te^{2t}+e^{t} \\<br />\end{pmatrix})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
