Exercice rigolo ^^
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 22 Aoû 2010, 15:51
par egan » 22 Aoû 2010, 15:51
Salut,
Je vous propose cet exo. Je ne sais pas du tout s'il s'agit d'un classique ou non mais je l'ai trouvé marrant.
Déterminer la borne inférieure de l'ensemble suivant:
)^2 dx \quad : \quad a,b \in \mathbb{R} \})
Amusez-vous bien. ^^
@+ Boris.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 22 Aoû 2010, 15:56
par Le_chat » 22 Aoû 2010, 15:56
Yop!
Je connais cet exo, je crois en effet que c'est un classique (enfin quand on voit la tête de l'intégrale...)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 22 Aoû 2010, 16:08
par girdav » 22 Aoû 2010, 16:08
Je pense aussi qu'il s'agit d'un classique : penser en terme de produit scalaire.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Aoû 2010, 16:09
par Zweig » 22 Aoû 2010, 16:09
Un classique ... quand on a déjà vu comment on pouvait appliquer les espaces euclidiens dessus :we:.
-
mathelot
 par mathelot » 22 Aoû 2010, 16:17
par mathelot » 22 Aoû 2010, 16:17
Bonjour,
conjecture:un petit croquis: la courbe de exponentielle dans le rectangle [0;1]x[1;e]
et une droite d'équation y=ax+b
Ce qui a l'aire de minimiser la différence d'aires est la droite horizontale (a=0)
passant par la valeur moyenne
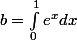
on développe et on fait

, M'sieur ? :we:
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 22 Aoû 2010, 18:24
par egan » 22 Aoû 2010, 18:24
En effet, ça se fait très bien avec les euclidiens. Il faut s'interresser à la distance de exp à l'espace vectoriel des fonctions affines.
J'ai trouvé une autre méthode beaucoup plus bourrine. Je me suis servi de Maple pour les calculs. On calcule l'intégrale pour des valeurs quelconques de a et de b. On se retrouve alors avec une fonction f de deux variables pour l'intégrale. On cherche les extremums possibles en résolvant le système qui correspond à l'annulation des deux dérivées partielles. On trouve qu'il y a bien un extremum en (a_0;b_0). L'étude du signe de f(a_0+u;b_0+v)-f(a_0;b_0) en fonction du (u;v) nous montre bien que cette expression est toujours positive ou nulle.
Mathelot, je ne comprends pas trop ce que tu fais.
-
mathelot
 par mathelot » 22 Aoû 2010, 18:44
par mathelot » 22 Aoû 2010, 18:44
egan a écrit:Mathelot, je ne comprends pas trop ce que tu fais.
je fais de l'analyse niveau Terminale S. un dessin de la courbe exponentielle
dans le rectangle plan
 \in [0;1] \times [1;e])
un segment de droite quelconque situé dans ce rectangle et ..résolution visuelle
je conjecture alors : a=0 et b=valeur moyenne de "exponentielle"
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 22 Aoû 2010, 19:55
par egan » 22 Aoû 2010, 19:55
a n'est pas égal à 0 dans la solution.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2010, 09:48
par girdav » 23 Aoû 2010, 09:48
On commence par chercher

et

tels que
)
est orthogonal à
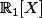
pour le produit scalaire
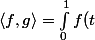g(t) dt)
. Il faut donc que
)
soit orthogonal à la fois à
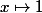
et à
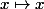
.
,1\rangle&=\int_0^1(e^x-(ax+b))dx\\<br />&=e-1-\fr a2-b<br />\end{align})
donc on obtient la condition
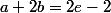
. Puis :
,x\rangle&=\int_0^1(e^x-(ax+b))xdx\\<br />&=\int_0^1xe^x dx-\fr a3-\fr b2\\<br />&=[xe^x]_0^1-\int_0^1 e^xdx-\fr a3-\fr b2 \\<br />&=e-(e-1)-\fr a3-\fr b2\\<br />&=1-\fr a3-\fr b2<br />\end{align})
donc on obtient que
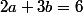
.
Il reste ensuite à résoudre le système puis à calculer le carré de la norme de
)
avec les

et

ainsi trouvés.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités