Espaces vectoriels
14 messages
- Page 1 sur 1
Espaces vectoriels
]Bonjour,
Je suis nouveau sur ce forum et je vous sollicite afin d'obtenir un peu d'aide sur certains problèmes, notamment les espaces vectoriels.
Je suis inscrit à un MOOC sur EDX (Algèbre linéaire) afin de monter en compétences mais je suis heurté à un petit problème sur les espaces vectoriels.
Je vous joins une capture d'écran du problème posé:
https://www.casimages.com/i/210912010758636099.jpg.html
Selon moi, seuls les deux derniers exemples sont des sous-espaces vectoriels de R3 mais d'après le site, ce n'est pas la bonne réponse...
Est-ce que quelqu'un pourrait éclaircir la situation?
Merci de votre aide!
Je suis nouveau sur ce forum et je vous sollicite afin d'obtenir un peu d'aide sur certains problèmes, notamment les espaces vectoriels.
Je suis inscrit à un MOOC sur EDX (Algèbre linéaire) afin de monter en compétences mais je suis heurté à un petit problème sur les espaces vectoriels.
Je vous joins une capture d'écran du problème posé:
https://www.casimages.com/i/210912010758636099.jpg.html
Selon moi, seuls les deux derniers exemples sont des sous-espaces vectoriels de R3 mais d'après le site, ce n'est pas la bonne réponse...
Est-ce que quelqu'un pourrait éclaircir la situation?
Merci de votre aide!
Re: Espaces vectoriels
Bonjour,
Ton scan est difficilement lisible. Les intervenants feraient sans doute plus d'effort si, de ton côté, tu prenais la peine de recopier l'énoncé qui n'a pas l'air si long.
Ton scan est difficilement lisible. Les intervenants feraient sans doute plus d'effort si, de ton côté, tu prenais la peine de recopier l'énoncé qui n'a pas l'air si long.
Re: Espaces vectoriels
Voici l'énoncé:
Déterminer, parmi les sous-ensembles suivants de R3, lesquels sont des sous-espaces vectoriels:
- L'ensemble W1 = {(t,t,u): t,u appartient à R}
- L'ensemble W2 = {(1+t,2t,3t): t appartient à R}
- L'ensemble W3 = {(x,y,z): x,y,z appartient à R, x²+y²+z² = 0}
- L'ensemble W4 = {(x,y,z): x,y,z appartient à R, x²+y²-z² = 0}
Merci!
Déterminer, parmi les sous-ensembles suivants de R3, lesquels sont des sous-espaces vectoriels:
- L'ensemble W1 = {(t,t,u): t,u appartient à R}
- L'ensemble W2 = {(1+t,2t,3t): t appartient à R}
- L'ensemble W3 = {(x,y,z): x,y,z appartient à R, x²+y²+z² = 0}
- L'ensemble W4 = {(x,y,z): x,y,z appartient à R, x²+y²-z² = 0}
Merci!
Re: Espaces vectoriels
Seuls le premier et le troisième sont des sous-espaces vectoriels de 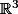 . Pour le troisième, c'est un peu un piège.
. Pour le troisième, c'est un peu un piège.
Peux-tu expliquer ta réponse ?
Peux-tu expliquer ta réponse ?
Re: Espaces vectoriels
Merci de ta réponse!
Pour moi, j'avais un doute sur la première réponse car je ne savais pas comment justifier la stabilité par l'addition et la multiplication. La deuxième proposition ne contient pas le vecteur nul, donc je l'ai éliminé. Enfin, je pensais les deux dernières propositions correctes car elles satisfaisaient les trois critères (contient le vecteur nul, stabilité de l'addition et de la multiplication par un scalaire), mais d'après ta réponse, je me suis trompé sur la dernière proposition.
Merci de ton aide!
Pour moi, j'avais un doute sur la première réponse car je ne savais pas comment justifier la stabilité par l'addition et la multiplication. La deuxième proposition ne contient pas le vecteur nul, donc je l'ai éliminé. Enfin, je pensais les deux dernières propositions correctes car elles satisfaisaient les trois critères (contient le vecteur nul, stabilité de l'addition et de la multiplication par un scalaire), mais d'après ta réponse, je me suis trompé sur la dernière proposition.
Merci de ton aide!
Re: Espaces vectoriels
Edit :Non il n'y est pas
je le vois pourtant
(ne pas tenir compte de ma réponse)
fredkron a écrit: La deuxième proposition ne contient pas le vecteur nul, donc je l'ai éliminé.
je le vois pourtant
(ne pas tenir compte de ma réponse)
Re: Espaces vectoriels
azf a écrit:fredkron a écrit: La deuxième proposition ne contient pas le vecteur nul, donc je l'ai éliminé.
je le vois pourtant
Alors il y a quelque chose que je n'ai pas compris...
Pour moi, dans R3, le vecteur nul s'écrit {0,0,0}.
Sachant que W2 est définit comme (1+t,2t,3t), on obtient: (1,0,0), en remplaçant t par 0.
Donc, j'ai conclut peut être à tort, que ce sous-ensemble ne contenait pas le vecteur nul car (1,0,0) est différent de (0,0,0).
Ah, trop tard ^^
Re: Espaces vectoriels
GaBuZoMeu a écrit:Revois si W4 est stable par addition !
Alors si je ne me trompe pas:
soit u(1,1,\sqrt{2}) \in W4
soit v(2,2,2\sqrt{2}) \in W4
Alors u+v=(3,3,2\sqrt{2}) \in W4
En remplaçant, on a: 3²+3²-(2\sqrt{2})=9+9-8=10, donc différent de 0.
Re: Espaces vectoriels
Ton contre-exemple ne marche pas (normal, tu as pris deux vecteurs colinéaires). Essaie d'en trouver un qui marche !
Re: Espaces vectoriels
GaBuZoMeu a écrit:Ton contre-exemple ne marche pas (normal, tu as pris deux vecteurs colinéaires). Essaie d'en trouver un qui marche !
Oui bien vu!
soit u(0,1,1) et v(1,0,1).
La somme de ces 2 vecteurs vaut (1,1,2).
En remplaçant dans l'équation, on a :
1²+1²-(2²)=-2, donc différent de 0.
Merci de votre aide!
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
