Equation fonctionnelle

[zigroful]

Bonjour à tous,
J'ai une équation fonctionnelle que je n'arrive pas à résoudre.
Je cherche à démontrer que toutes les fonctions f de R dans R, telle que:
Quelque soit x ,a,b appartenant à R : f(f(x)+ax+b)=x (0)
sont bijectives.

Pour la surjectivité: Soit x dans R, démontrons qu'il existe z appartenant à R tel que f(z)=x.
En effet, il suffit de prendre z=f(x)+ax+b, et l'on a bien, d'après (0) f(z)=x.

Mais je bute sur l'injectivité. Je ne vois pas comment démontrer que si l'on prend x1 différent de x2, on a nécessairement f(x1) différent de f(x2) !
Quelqu'un a-t-il une idée ?

[catamat]

Bonjour

Il semble plus simple d'utiliser la contraposée
Si alors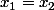

Ceci dit je pense que les quantificateurs sont mal positionnés. j'écrirais plutôt :

Pour tout a et b réels, la fonction f telle que pour tout réel x, f(f(x)+ax+b)=x est une bijection

[zigroful]

Mais même en prenant f(x1)=f(x2), on pourrait écrire f(f(x1)+ax1+b)=x1 et f(f(x2)+ax2+b)=x2 et f(x1)=f(x2) permettrait d'écrire :
f(f(x1)+ax1+b)=x1 et f(f(x1)+ax2+b)=x2, mais les arguments des 2 fonctions f (càd f(x1)+ax1+b et f(x1)+ax2+b) ne sont pas les mêmes puisque ax1 est différent de ax2 à priori. Je ne vois donc pas ce qui permettrai de dire que x1=x2

[zigroful]

Merci catamat d'avoir répondu à ma question.

j'ai pensé à poser : g(x)=f(x)+ax+b (2)
L'équation (0) s'écrit alors, f(g(x))=x (3) càd fog=I I étant l'identité.
Il resterait à démontrer que gof=I
Or g(f(x))=f(f(x))+af(x)+b (4) en remplaçant x par f(x) dans (0)
Par ailleurs en appliquant f à (3) on a f(f(g(x))=f(x)=g(x)-ax-b (d'après (2)) et ax=af(g(x)) d'après (3)
D'où f(f(g(x))=g(x)-af(g(x))-b
càd f(f(g(x))+af(g(x))+b= g(x) (5)
En posant z=g(x) , on obtient f(f(z))+af(z)+b=z (6)
mais (4) donne g(f(z))=f(f(z))+af(z)+b (7)
En combinant (6) et (7), on obtient g(f(z))=z, càd gof=I
Puisqu'on a fog=gof=I , on conclut que f est bijective et g serait la fonction réciproque de f ?
Je ne sais si ce raisonnement est rigoureux.
Peux-tu me le dire catamat ?

[catamat]

Perso, je n'ai pas décelé d'erreurs dans le calcul... donc pour moi c'est OK.

Il y a peut être plus simple, si quelqu'un a une idée...

Juste un détail

Or g(f(x))=f(f(x))+af(x)+b (4) en remplaçant x par f(x) dans (0)

C'est en remplaçant dans (2) en fait

[zigroful]

Oui ! très juste, c'est en remplaçant dans (2) et non dans (0).
Merci pour votre réponse, catamat

[Ben314]

Salut,
J'ai pas regardé le reste, mais si ta preuve est basé sur ça :

En posant z=g(x) . . . on obtient g(f(z))=z, càd gof=I.

alors c'est incomplet vu que tu ne prouve l'égalité g(f(z))=z que pour certains réels z et pas pour tous.
Il faudrait avoir la surjectivité de la fonction g pour que ce soit O.K.