Entiers naturels ayant beaucoup de diviseurs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 15 Fév 2010, 20:29
par mathelot » 15 Fév 2010, 20:29
Bonjour,
quand on regarde les diviseurs d'un entier N comme les points (m;n)
du plan situés sur l'hyperbole d'équation xy=N=mn
on se pose la question:
quels sont les entiers qui ont "beaucoup" de diviseurs ? le plus de diviseurs ?
sont-ce les entiers de la forme
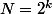
(ils ont
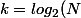+1)
diviseurs) ? sont-ce eux, qui ont relativement le plus de diviseurs ?
merci.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Fév 2010, 20:32
par Doraki » 15 Fév 2010, 20:32
Pour avoir 2^k diviseurs, on peut prendre le produit des k premiers nombres premiers.
Je pense que c'est plus petit que de prendre 2^(2^k-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
