Développement en série entière de ln(1+x²)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Julien57160
- Membre Naturel
- Messages: 25
- Enregistré le: 24 Avr 2010, 17:20
-
 par Julien57160 » 24 Avr 2010, 17:28
par Julien57160 » 24 Avr 2010, 17:28
Bonjour,
J'ai a réaliser le DSE de ln(1+x²)... et je ne suis pas sur d'avoir compris le processus à l'aide de la formule f(x)=a0+a1(x)+a2(x²)+...+anx^n :cry:
Merci pour votre aide.
-
Julien57160
- Membre Naturel
- Messages: 25
- Enregistré le: 24 Avr 2010, 17:20
-
 par Julien57160 » 24 Avr 2010, 18:18
par Julien57160 » 24 Avr 2010, 18:18
Oui j'ai le résultat de ln(1+x) mais je ne comprends pas comment on le trouve.
-
greg78
- Membre Relatif
- Messages: 142
- Enregistré le: 08 Fév 2009, 11:26
-
 par greg78 » 24 Avr 2010, 18:22
par greg78 » 24 Avr 2010, 18:22
Par intégration terme à terme du DSE de
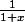
-
Julien57160
- Membre Naturel
- Messages: 25
- Enregistré le: 24 Avr 2010, 17:20
-
 par Julien57160 » 24 Avr 2010, 19:14
par Julien57160 » 24 Avr 2010, 19:14
J'ai bien compris qu'il fallait intégrer terme à terme le DSE de ln(1+x) qui est égal à:
1/(1+x) = 1 -x + x² - x^3 + .... + (-1)^n*x^n
ce que je ne comprends pas c'est comment on trouve:
1 -x + x² - x^3 + .... + (-1)^n*x^n
Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Avr 2010, 19:31
par Ben314 » 24 Avr 2010, 19:31
Si je t'écrit :
1/(1-q)=1+q+q²+q^3+...
ça te dit rien non plus ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Julien57160
- Membre Naturel
- Messages: 25
- Enregistré le: 24 Avr 2010, 17:20
-
 par Julien57160 » 25 Avr 2010, 11:46
par Julien57160 » 25 Avr 2010, 11:46
Non pas vraiment.
Merci quand meme
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Avr 2010, 11:50
par Nightmare » 25 Avr 2010, 11:50
Salut,
rapidement, si je note S=1+y+y^2+y^3+... on a yS=y+y^3+...=S-1
Donc S=1/(1-y) puis prendre y=-x.
-
Heure
- Membre Naturel
- Messages: 44
- Enregistré le: 04 Avr 2010, 19:51
-
 par Heure » 25 Avr 2010, 11:55
par Heure » 25 Avr 2010, 11:55
Suites géométriques?
-
Julien57160
- Membre Naturel
- Messages: 25
- Enregistré le: 24 Avr 2010, 17:20
-
 par Julien57160 » 27 Avr 2010, 22:09
par Julien57160 » 27 Avr 2010, 22:09
D'accord je me suis remis dedans et en effet c'est la somme dune suite geometrique. merci a tous
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
