Déterminer un noyau Ker, sa base et sa dimension
62 messages
- Page 1 sur 4 - 1, 2, 3, 4
Déterminer un noyau Ker, sa base et sa dimension
Bonjour à tous chers amis,
J'ai une application de R4 dans R3 tq:
f(u)=f(x,y,z,t)=(x-y+z, 2x-y+3t, -2x+2y-2z)
On demande: "Déterminer Ker f. En donner une base et une dimension".
J'ai donc calculé le système
x-y+z=0
2x-y+3t=0
-2x+2y-2z=0
Je trouve comme solutions z=-x+y,
t=-2x/3 + 1y/3 et anecdotiquement z=3t+x.
Seulement voilà, ça ne me donne pas mon noyau Ker (?!)
Comment faut il faire pour sortir le fameux noyau des solutions (?)
Merci d'avance
J'ai une application de R4 dans R3 tq:
f(u)=f(x,y,z,t)=(x-y+z, 2x-y+3t, -2x+2y-2z)
On demande: "Déterminer Ker f. En donner une base et une dimension".
J'ai donc calculé le système
x-y+z=0
2x-y+3t=0
-2x+2y-2z=0
Je trouve comme solutions z=-x+y,
t=-2x/3 + 1y/3 et anecdotiquement z=3t+x.
Seulement voilà, ça ne me donne pas mon noyau Ker (?!)
Comment faut il faire pour sortir le fameux noyau des solutions (?)
Merci d'avance
Modifié en dernier par Cambacérès le 28 Sep 2021, 12:49, modifié 1 fois.
Re: Déterminer un noyau Ker, sa base et sa dimension
Bonjour,
voici mes calculs (j'espère qu'il n' y a pas d'erreur, vérifiez)
x-y+2z =0, (1)
2x-y+3t=0, (2)
-2x+2y-2z =0 (3)
(3) donne -x+y-z =0 soit y =x+z,
-on remplace dans (1) on a x-x-z+2z =0 soit z=0 donc y=x
-on remplace dans (2) on a 2x-x+z+3t=0 soit x+3t=0 soit t=-x/3
le vecteur qui engendre le noyau est v=(x,x,0,_x/3)=x(1,1,0,-1/3)
voici mes calculs (j'espère qu'il n' y a pas d'erreur, vérifiez)
x-y+2z =0, (1)
2x-y+3t=0, (2)
-2x+2y-2z =0 (3)
(3) donne -x+y-z =0 soit y =x+z,
-on remplace dans (1) on a x-x-z+2z =0 soit z=0 donc y=x
-on remplace dans (2) on a 2x-x+z+3t=0 soit x+3t=0 soit t=-x/3
le vecteur qui engendre le noyau est v=(x,x,0,_x/3)=x(1,1,0,-1/3)
Re: Déterminer un noyau Ker, sa base et sa dimension
erratum :
un vecteur du noyau est v=(x,x,0,-x/3)=x(1,1,0,-1/3)
le vecteur qui engendre le noyau est (1,1,0,-1/3)
un vecteur du noyau est v=(x,x,0,-x/3)=x(1,1,0,-1/3)
le vecteur qui engendre le noyau est (1,1,0,-1/3)
Re: Déterminer un noyau Ker, sa base et sa dimension
Bonjour cher Phyelec,
Malheureusement je crois qu'il y a une erreur dans votre système
En effet on a dans l'énoncé x-y+z=0 et non. x-y+2z=0comme vous l'écrivez.
Ce qui change beaucoup parce qu'injecter y=x+z dedans nous donne alors 0=0.
De la même façon l'injecter dans -2x+2y-2z=0 nous donne l'instructif 0=0
Enfin bref les deux seules infos qu'on a sont:
y=x+z
t=-2/3x +1/3y
La question c'est comment en sortir un noyau
Malheureusement je crois qu'il y a une erreur dans votre système
En effet on a dans l'énoncé x-y+z=0 et non. x-y+2z=0comme vous l'écrivez.
Ce qui change beaucoup parce qu'injecter y=x+z dedans nous donne alors 0=0.
De la même façon l'injecter dans -2x+2y-2z=0 nous donne l'instructif 0=0
Enfin bref les deux seules infos qu'on a sont:
y=x+z
t=-2/3x +1/3y
La question c'est comment en sortir un noyau
Re: Déterminer un noyau Ker, sa base et sa dimension
dans votre énoncé vous avez f(u)=f(x,y,z,t)=(x-y+2z, 2x-y+3t, -2x+2y-2z)?!
Re: Déterminer un noyau Ker, sa base et sa dimension
Aie aie aie vous avez raison j'ai fait une terrible faute de frappe.
On a (x-y+z, 2x-y+3t, -2x+2y-2z)
Si on exprime tous les termes en fonction de y on a:
y=x+z
y=2x+3t
y=2z-3t
Donc
x=z-3t
x=y-z
x=(y-3t)/2
z=y-x
z=x+3t
z=(y+3t)/2
t=(2z-y)/3
t=(z-x)/3
t=(y-2x)/3
On a (x-y+z, 2x-y+3t, -2x+2y-2z)
Si on exprime tous les termes en fonction de y on a:
y=x+z
y=2x+3t
y=2z-3t
Donc
x=z-3t
x=y-z
x=(y-3t)/2
z=y-x
z=x+3t
z=(y+3t)/2
t=(2z-y)/3
t=(z-x)/3
t=(y-2x)/3
Re: Déterminer un noyau Ker, sa base et sa dimension
le système est :
x-y+z =0
2x-y+3t=0
-2x+2y-2z=0
écrit autrement :
x - y+z =0 => y=x+z
-x + y-z =0 => y=x+z
2x-y+ 3t=0 => t= (y-2x)/3 =(z-x)/3
donc si mes calculs sont bons un vecteur du noyau s'écrit v=(x,x+z,z,(z-x)/3)=x(1,1,-1/3)+z(0,1,1/3)
x-y+z =0
2x-y+3t=0
-2x+2y-2z=0
écrit autrement :
x - y+z =0 => y=x+z
-x + y-z =0 => y=x+z
2x-y+ 3t=0 => t= (y-2x)/3 =(z-x)/3
donc si mes calculs sont bons un vecteur du noyau s'écrit v=(x,x+z,z,(z-x)/3)=x(1,1,-1/3)+z(0,1,1/3)
Re: Déterminer un noyau Ker, sa base et sa dimension
Merci beaucoup cher Phyelec, effectivement on trouve bien avec votre formule:
x(1,0,-1,-2/3) et y(0,1,1,1/3)
Une question, comment avez vous trouvé cette chouette formule:
(x,x+z,z,(z-x)/3)?
x(1,0,-1,-2/3) et y(0,1,1,1/3)
Une question, comment avez vous trouvé cette chouette formule:
(x,x+z,z,(z-x)/3)?
Re: Déterminer un noyau Ker, sa base et sa dimension
vous avez trouvez x(1,0,-1,-2/3) et y(0,1,1,1/3) avec le système z=y-x et t=(y-2x)/3, ici t et z sont fonctions de x et y quelconques.
comment je trouve (x,x+z,z,(z-x)/3) :
le système d'équation me donne y=x+z et t= (y-2x)/3=(x+z-2x)/3=(z-x)/3, ici t et y sont fonctions de x et z quelconques.
pour un vecteur v(x,y,z,t) du noyau je choisis x et z et puis y et t sont donnés par y=x+z et t= (z-x)/3.
v=(x,y,z,t)=(x,x+z,z,(z-x)/3)=(x,x,0,-x/3)+(0,z,z,z/3)=x(1,1,0,-1/3)+z(0,1,1,1/3)
comment je trouve (x,x+z,z,(z-x)/3) :
le système d'équation me donne y=x+z et t= (y-2x)/3=(x+z-2x)/3=(z-x)/3, ici t et y sont fonctions de x et z quelconques.
pour un vecteur v(x,y,z,t) du noyau je choisis x et z et puis y et t sont donnés par y=x+z et t= (z-x)/3.
v=(x,y,z,t)=(x,x+z,z,(z-x)/3)=(x,x,0,-x/3)+(0,z,z,z/3)=x(1,1,0,-1/3)+z(0,1,1,1/3)
Re: Déterminer un noyau Ker, sa base et sa dimension
Merci de tout coeur pour cette explication lumineuse!
Mais du coup la réponse attendue par les correcteurs est elle avec x et y ou x et z (?)
Pour la base canonique, comment peut on la sortir de nos résultats.
J'ai un copain qui a trouvé {(1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0)} mais je ne vois pas comment il a pu faire(?)
Amicalement,
Mais du coup la réponse attendue par les correcteurs est elle avec x et y ou x et z (?)
Pour la base canonique, comment peut on la sortir de nos résultats.
J'ai un copain qui a trouvé {(1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0)} mais je ne vois pas comment il a pu faire(?)
Amicalement,
Re: Déterminer un noyau Ker, sa base et sa dimension
Et à propos du noyau, aurait on pu choisir au lieu de (x,y) ou (x,z) quelque chose comme (x,y,z) ou (t,x,z) ou (z,t,x,y) ou juste t, enfin toute combinaison (?)
Re: Déterminer un noyau Ker, sa base et sa dimension
kerf a plusieurs bases ( c'est logique car une base une famille libre de vecteurs qui engendre un espace vectoriel).
On ne peut pas prendre " toute combinaison" cela dépend du système à résoudre.
ici on a :
y=x+z
t=(y -2x)/3
4 inconnues 2 équations. Il faut donc en fixer 2 pour trouver les 2 autres.
On ne peut pas prendre " toute combinaison" cela dépend du système à résoudre.
ici on a :
y=x+z
t=(y -2x)/3
4 inconnues 2 équations. Il faut donc en fixer 2 pour trouver les 2 autres.
Re: Déterminer un noyau Ker, sa base et sa dimension
Dans votre exercice le question est "Déterminer Ker f. En donner une base et une dimension".
Donc vous donnez une base, celle que vous voulez pour répondre.
Donc vous donnez une base, celle que vous voulez pour répondre.
Re: Déterminer un noyau Ker, sa base et sa dimension
Merci pour cette explication limpide!
Pour la base canonique (1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0), comment extrait on ces valeurs qui n'ont rien à voir avec notre noyau(?)
Merci encore:)
Pour la base canonique (1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0), comment extrait on ces valeurs qui n'ont rien à voir avec notre noyau(?)
Merci encore:)
Re: Déterminer un noyau Ker, sa base et sa dimension
Enfin je ne vois pas à quoi correspondent ces valeurs, pourquoi 4 couples et pourquoi (0,3,0) par exemple (?)
Re: Déterminer un noyau Ker, sa base et sa dimension
Vous ne faites pas état d'une question sur la une base canonique et si oui de quoi?
A ma connaissance les vecteurs canoniques sont par exemple pour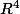 e1=(1,0,0,0),e2=(0,1,0,0),e3=(0,0,1,0),e4=(1,0,0,0).
e1=(1,0,0,0),e2=(0,1,0,0),e3=(0,0,1,0),e4=(1,0,0,0).
A ma connaissance les vecteurs canoniques sont par exemple pour
Re: Déterminer un noyau Ker, sa base et sa dimension
peut-être vous demande t-on d'exprimer les vecteurs de la base de kerf en fonction des vecteurs canonique de 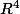 ?
?
Re: Déterminer un noyau Ker, sa base et sa dimension
Merci beaucoup pour cette réponse, oui je pensais aussi aux vecteurs canoniques mais il semble qu'il y ait une subtilité.
Voici l'énoncé :
Soit f une application linéaire de R4 dans R3 tel que
f(u)=f(x,y,z,t)=(x-y+z,2x-y+3t,-2x+2y-2z)
a)Montrer que f est une application linéaire de R4 dans R3
J'ai montré que f(u+v)=f(u)+f(v) et f(a u)=a f(u).
b) Déterminer Ker de f. En donner une base et une dimension
x(1,0,-1,-2/3) et y(0,1,1,1/3)
Dim Ker(f)=2
c)Quelle est la dimension de f(R4)?
Comme Dim ker(f)=2, on a Dim(f)=Dim(R4)-Dim Ker(f) qui fait 2, d'où Dim(f)=2.
d) Déterminer une base f(R4)
Je bloque. Un copain a trouvé (1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0).
Je ne vois pas comment il a fait.
e)f est elle injective, bijective, surjective
Comme Ker(f) différent de 0, f n'est pas injective
Comme Dim f(R4)=2 et qu'elle est differente de Dim(R4)=4,
f n'est pas surjective. Je ne suis pas sûr que ce soit bien justifié.
Comme f n'est ni injective ni surjective elle n'est pas bijective.
f)Calculer la matrice A représentant f dans les bases canoniques de R4 et R3
Je prends les 4 vecteurs que mon copain a trouvé à la question d) sur la base de f(R4) et je les mets en colonne. Le seul problème c'est que je ne sais pas comment il a trouvé son résultat
Voici l'énoncé :
Soit f une application linéaire de R4 dans R3 tel que
f(u)=f(x,y,z,t)=(x-y+z,2x-y+3t,-2x+2y-2z)
a)Montrer que f est une application linéaire de R4 dans R3
J'ai montré que f(u+v)=f(u)+f(v) et f(a u)=a f(u).
b) Déterminer Ker de f. En donner une base et une dimension
x(1,0,-1,-2/3) et y(0,1,1,1/3)
Dim Ker(f)=2
c)Quelle est la dimension de f(R4)?
Comme Dim ker(f)=2, on a Dim(f)=Dim(R4)-Dim Ker(f) qui fait 2, d'où Dim(f)=2.
d) Déterminer une base f(R4)
Je bloque. Un copain a trouvé (1,2,-2),(-1,-1,2),(1,0,-2)(0,3,0).
Je ne vois pas comment il a fait.
e)f est elle injective, bijective, surjective
Comme Ker(f) différent de 0, f n'est pas injective
Comme Dim f(R4)=2 et qu'elle est differente de Dim(R4)=4,
f n'est pas surjective. Je ne suis pas sûr que ce soit bien justifié.
Comme f n'est ni injective ni surjective elle n'est pas bijective.
f)Calculer la matrice A représentant f dans les bases canoniques de R4 et R3
Je prends les 4 vecteurs que mon copain a trouvé à la question d) sur la base de f(R4) et je les mets en colonne. Le seul problème c'est que je ne sais pas comment il a trouvé son résultat
Re: Déterminer un noyau Ker, sa base et sa dimension
votre question est "Déterminer une base f(R4)", donc il n'est pas question de canonique.
Dim(f) =2 donc sa base est constituée de 2 vecteurs libres appartenant à Im(f).
Deux manières de faire :
1) calculer Im(f)= Vect(f(e1),f(e2)f(e3),f(e3),f(e4) c'est la méthode de votre ami.
vous avez 4 vecteurs qui sont une famille génératrice de Im(f), il faut vérifier qu'ils sont linéairement indépendants pour prouvez que c'est une base de Im(f). Au passage, comme à la question précédente vous avez calculé Dim(f) vous savez que c'est 4 vecteurs ne forment pas une base de Im(f), il en faut 2.
2)Vous cherchez 2 vecteurs linéairement indépendants de Im(f).
Dim(f) =2 donc sa base est constituée de 2 vecteurs libres appartenant à Im(f).
Deux manières de faire :
1) calculer Im(f)= Vect(f(e1),f(e2)f(e3),f(e3),f(e4) c'est la méthode de votre ami.
vous avez 4 vecteurs qui sont une famille génératrice de Im(f), il faut vérifier qu'ils sont linéairement indépendants pour prouvez que c'est une base de Im(f). Au passage, comme à la question précédente vous avez calculé Dim(f) vous savez que c'est 4 vecteurs ne forment pas une base de Im(f), il en faut 2.
2)Vous cherchez 2 vecteurs linéairement indépendants de Im(f).
62 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
