Que pensez-vous de cette démonstration de : p divise
Démonstration p divise (p k)
16 messages
- Page 1 sur 1
Démonstration p divise (p k)
Bonsoir,
Que pensez-vous de cette démonstration de : p divise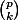 pour
pour 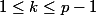 , lu dans un livre de maths :
, lu dans un livre de maths :
!}) donc
donc !\binom{p}{k}) . Ainsi p divise
. Ainsi p divise !\binom{p}{k}) . Or comme
. Or comme 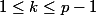 alors p ne divise pas k! (sinon p divise l'un des facteurs de k! mais ils sont tous
alors p ne divise pas k! (sinon p divise l'un des facteurs de k! mais ils sont tous 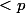 ). De même p ne divise pas (p-k)!, donc par le lemme d'Euclide p divise
). De même p ne divise pas (p-k)!, donc par le lemme d'Euclide p divise 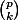 .
.
Que pensez-vous de cette démonstration de : p divise
Re: Démonstration p divise (p k)
Salut,
Modulo bien sûr de préciser que p désigne un nombre premier, ça me semble effectivement être la preuve la plus fréquente qu'on trouve sur le sujet.
Le seul truc, c'est qu'il faut bien sûr avoir préalablement démontré que!}) est entier mais en général lorsque l'on en est à démontrer ce type de résultat, ça fait un moment qu'on sait que c'est vrai.
est entier mais en général lorsque l'on en est à démontrer ce type de résultat, ça fait un moment qu'on sait que c'est vrai.
Modulo bien sûr de préciser que p désigne un nombre premier, ça me semble effectivement être la preuve la plus fréquente qu'on trouve sur le sujet.
Le seul truc, c'est qu'il faut bien sûr avoir préalablement démontré que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Démonstration p divise (p k)
Ah bien sûr, je n'avais pas fait attention que p désigne un nombre premier (ouf), ce n'était pas rappelé dans la démo. Mais il faut quand même démontrer que le coefficient binomial est un entier (ce qui me paraît une autre paire de manches). Merci !
Re: Démonstration p divise (p k)
1) Concernant le fait que c'est un entier, je pense que dans la majorité de la littérature, 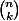 est défini comme étant "le nombre de façon de choisir k objet parmi n" (qui est évidement un entier) puis on montre ensuite que
est défini comme étant "le nombre de façon de choisir k objet parmi n" (qui est évidement un entier) puis on montre ensuite que !}) .
.
Il y a plusieurs arguments possibles, l'un d'entre eux consistant à privilégier un des éléments parmi les n, puis à dire "soit on le prend, soit on le prend pas" pour en déduire que) et terminer par une récurrence sur
et terminer par une récurrence sur  .
.
2) On peut aussi définir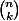 comme le coefficient en
comme le coefficient en 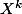 dans le développement de
dans le développement de ^n) (qui de nouveau est clairement entier) puis en déduire (c'est immédiat) que
(qui de nouveau est clairement entier) puis en déduire (c'est immédiat) que ) est vrai et terminer par la même récurrence qu'au 1)
est vrai et terminer par la même récurrence qu'au 1)
3) Enfin, si on pose directement!}) je pense que le plus rapide pour montrer que c'est un entier est de nouveau de commencer par montrer que
je pense que le plus rapide pour montrer que c'est un entier est de nouveau de commencer par montrer que ) est vrai puis de faire une récurrence sur
est vrai puis de faire une récurrence sur  .
.
Bref, j'aurais tendance à penser que, quelque soit la définition choisie, l'un des premier trucs à démontrer (voire même LE premier), c'est la propriété) (ce qui en plus permet de construire le triangle de Pascal).
(ce qui en plus permet de construire le triangle de Pascal).
Il y a plusieurs arguments possibles, l'un d'entre eux consistant à privilégier un des éléments parmi les n, puis à dire "soit on le prend, soit on le prend pas" pour en déduire que
2) On peut aussi définir
3) Enfin, si on pose directement
Bref, j'aurais tendance à penser que, quelque soit la définition choisie, l'un des premier trucs à démontrer (voire même LE premier), c'est la propriété
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Démonstration p divise (p k)
Bonjour et merci Ben314 ! Il faudrait graver ce que tu écris dans le marbre.
Celle qui me convainc le plus est bien sûr la dernière. On pose!}) , on démontre la formule de récurrence sur n (*) pour
, on démontre la formule de récurrence sur n (*) pour 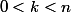 , et après avoir remarqué que
, et après avoir remarqué que 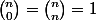 pour tout n, cela montre que ces coefficients binomiaux sont bien des entiers.
pour tout n, cela montre que ces coefficients binomiaux sont bien des entiers.
Bien sûr par le 1), le nombre de façons de choisir k objets parmi n, c'est bien un entier, et par le raisonnement logique on montre le coefficient binomial, mais il y a quelque chose de gênant de le montrer ainsi.
Celle qui me convainc le plus est bien sûr la dernière. On pose
Bien sûr par le 1), le nombre de façons de choisir k objets parmi n, c'est bien un entier, et par le raisonnement logique on montre le coefficient binomial, mais il y a quelque chose de gênant de le montrer ainsi.
Re: Démonstration p divise (p k)
Il y a peut être aussi ça :
Un produit de n entiers consécutifs, le plus petit valant au moins n, est divisible par n!
Un produit de n entiers consécutifs, le plus petit valant au moins n, est divisible par n!
Re: Démonstration p divise (p k)
nodgim a écrit:Il y a peut être aussi ça :
Un produit de n entiers consécutifs, le plus petit valant au moins n, est divisible par n!
Un produit de n entiers consécutifs est divisible par n, n-1, n-2, .... , 2, 1, ok, mais pourrais-tu donner une démonstration pour qu'il soit divisible par n! ?
Re: Démonstration p divise (p k)
Oui, et ce n'est pas difficile.
Dans la séquence des entiers consécutifs de 1 à n, un facteur premier élevé à la puissance k, p^k, arrive toujours au rang p^k. Dans toute autre suite qui commence à m, ce p^k apparait au pire à la position p^k depuis m. Donc [n/p^k] qui compte le nombre de p^k dans n! est plus petit ou égal que [n/p^k] dans la suite qui commence à m.
On ne peut donc pas avoir de facteurs manquants dans la suite qui commence à m par rapport à n!
Dans la séquence des entiers consécutifs de 1 à n, un facteur premier élevé à la puissance k, p^k, arrive toujours au rang p^k. Dans toute autre suite qui commence à m, ce p^k apparait au pire à la position p^k depuis m. Donc [n/p^k] qui compte le nombre de p^k dans n! est plus petit ou égal que [n/p^k] dans la suite qui commence à m.
On ne peut donc pas avoir de facteurs manquants dans la suite qui commence à m par rapport à n!
Re: Démonstration p divise (p k)
Par exemple 2^3 = 8 apparait au rang 8 dans la suite des entiers de 1 à 10. Alors que dans toute autre suite de 10 entiers consécutifs, 8 apparaitra, comme facteur premier, à un rang au plus égal à 7 unités du premier entier de la suite.
Re: Démonstration p divise (p k)
Je ne suis pas convaincu pas cet argument , le même diviseur pouvant être compté plusieurs fois . L'exercice "classique" fonctionne dans l'autre sens : en considérant une bonne combinaison , le produit de n entiers consécutifs est divisible par n! .
Imod
Imod
Re: Démonstration p divise (p k)
Oui, la combinatoire est la preuve la plus simple (quand on sait comment se calcule une combinaison).
Évidemment, le nombre de nombres que p^k divise dans la suite 1 à n est identique pour une autre suite de n entiers consécutifs. Mieux: il est facile de montrer que si le nombre de p présents dans une suite de n nombres consécutifs est supérieur au nombre de p dans la suite 1 à n, la différence n'est portée que par un seul nombre.
Évidemment, le nombre de nombres que p^k divise dans la suite 1 à n est identique pour une autre suite de n entiers consécutifs. Mieux: il est facile de montrer que si le nombre de p présents dans une suite de n nombres consécutifs est supérieur au nombre de p dans la suite 1 à n, la différence n'est portée que par un seul nombre.
Re: Démonstration p divise (p k)
Je comprend pas trop ce que tu veut dire :nodgim a écrit:Mieux: il est facile de montrer que si le nombre de p présents dans une suite de n nombres consécutifs est supérieur au nombre de p dans la suite 1 à n, la différence n'est portée que par un seul nombre.
- Déjà, je vois pas bien ce que signifie "le nombre de p présent dans la suite" : soit l'entier p est dans la suite de n nombres, (une seule fois évidement), soit il n'y est pas.
- Ensuite le "la différence n'est portée que par un seul nombre" que je comprend pas trop non plus, ça me fait penser à "LA goutte d'eau qui fait déborder le vase" : si le vase déborde, c'est pas la faute d'une goute en particulier, mais au fait qu'au total elles sont trop nombreuses.
Bref, tu peu clarifier ton truc ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Démonstration p divise (p k)
J'aurais dû préciser p présent comme facteur premier.
Je récapitule en espérant que ce sera plus clair.
n! se décompose en un produit de facteurs premiers. Pour compter la puissance d'un facteur premier p dans cette décomposition, on calcule la somme Sp = [n/p] + [n/p²] + [n/p^3]...
Dans la factorielle (m à m+n-1) !, on trouvera une puissance du facteur premier p au moins aussi forte. En effet, comme le 1er p^k dans n! est le nombre p^k lui même, et comme dans la suite des entiers naturels p^k apparait une fois en facteur premier tous les p^k entiers, alors p^k apparaitra dans la suite des entiers (m à m+n-1) au pire au rang m + p^k - 1. Ce seul constat suffit à prouver que que (m à m+n-1) ! divise n !
Selon la position de m, on pourra trouver dans les entiers (m à m + n - 1) un nombre de plus divisé par p que dans (1 à n). Par exemple, dans (1 à 9) le 5 n'est présent qu'une fois, alors qu'il est présent 2 fois dans (15 à 23) en 15 et 20.
Par ailleurs, si k est la puissance maximale telle que p^k divise un (ou plusieurs) nombres de (1 à n), alors dans l'intervalle (m à m+n-1) il ne peut pas exister 2 nombres divisibles par p^(k+1). Si tel était le cas, l'écart entre ces 2 nombres étant p^(k+1), inférieur à n, p^(k+1) se trouverait dans l'intervalle (1 à n).
Je récapitule en espérant que ce sera plus clair.
n! se décompose en un produit de facteurs premiers. Pour compter la puissance d'un facteur premier p dans cette décomposition, on calcule la somme Sp = [n/p] + [n/p²] + [n/p^3]...
Dans la factorielle (m à m+n-1) !, on trouvera une puissance du facteur premier p au moins aussi forte. En effet, comme le 1er p^k dans n! est le nombre p^k lui même, et comme dans la suite des entiers naturels p^k apparait une fois en facteur premier tous les p^k entiers, alors p^k apparaitra dans la suite des entiers (m à m+n-1) au pire au rang m + p^k - 1. Ce seul constat suffit à prouver que que (m à m+n-1) ! divise n !
Selon la position de m, on pourra trouver dans les entiers (m à m + n - 1) un nombre de plus divisé par p que dans (1 à n). Par exemple, dans (1 à 9) le 5 n'est présent qu'une fois, alors qu'il est présent 2 fois dans (15 à 23) en 15 et 20.
Par ailleurs, si k est la puissance maximale telle que p^k divise un (ou plusieurs) nombres de (1 à n), alors dans l'intervalle (m à m+n-1) il ne peut pas exister 2 nombres divisibles par p^(k+1). Si tel était le cas, l'écart entre ces 2 nombres étant p^(k+1), inférieur à n, p^(k+1) se trouverait dans l'intervalle (1 à n).
Re: Démonstration p divise (p k)
nodgim a écrit:n! se décompose en un produit de facteurs premiers. Pour compter la puissance d'un facteur premier p dans cette décomposition, on calcule la somme Sp = [n/p] + [n/p²] + [n/p^3]....
Dans la factorielle (m à m+n-1) !, on trouvera une puissance du facteur premier p au moins aussi forte. En effet, comme le 1er p^k dans n! est le nombre p^k lui même, et comme dans la suite des entiers naturels p^k apparait une fois en facteur premier tous les p^k entiers, alors p^k apparaitra dans la suite des entiers (m à m+n-1) au pire au rang m + p^k - 1.
Bonjour,
Je reprends mot à mot avec un exemple :
Dans la factorielle 12*13*14*15*16, on trouvera une puissance de 2 au moins aussi forte. En effet comme le 1er 2^k dans 5! est le nombre 2^k lui-même, c'est quoi k ?????
Re: Démonstration p divise (p k)
A part la dernière partie, k est pris dans un sens général, comme un entier quelconque non nul. Par exemple pour k=2 et p= 2, 2² = 4, et [5/4] = 1.
Dans toute autre suite de 5 entiers consécutifs, on trouvera au moins 1 nombre divisible par 4.
Dans toute autre suite de 5 entiers consécutifs, on trouvera au moins 1 nombre divisible par 4.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
