Calcul différentiel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marius1986
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Aoû 2009, 10:33
-
 par marius1986 » 01 Sep 2009, 14:55
par marius1986 » 01 Sep 2009, 14:55
Bien le bonjour à vous,
J'ai de sérieux problème avec un exercice que je cherche depuis 1e semaine et j(aimerai votre aide.
Voici l'EnoncéSoit E un e.v euclidien et f une aplication de classe

de E dans E telle que pour tt x et h de E,

où

est un réel strictement positif.
Question: En appliquant le théorème des accroissements finis aux fonctions
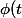=)
et
=\alphat)
, montrer que pour tout a et b de E on a:

Merci d'avance
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 01 Sep 2009, 15:31
par ToToR_2000 » 01 Sep 2009, 15:31
Bonjour,
il me semble qu'il existe un théorème des accroissements finis pour les fonctions à valeurs vectorielles, donc en l'appliquant, c'est vraiment immédiat...
Si tu ne le connais pas ou que tu n'as pas le droit de l'utiliser, et bien prends

et il existe c entre 0 et 1 tel que:
-\phi(0)=\phi^{'}(c))
en calculant cette dérivée, tu dois tomber sur

-
marius1986
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Aoû 2009, 10:33
-
 par marius1986 » 01 Sep 2009, 19:16
par marius1986 » 01 Sep 2009, 19:16
ToToR_2000 a écrit:Bonjour,
il me semble qu'il existe un théorème des accroissements finis pour les fonctions à valeurs vectorielles, donc en l'appliquant, c'est vraiment immédiat...
Si tu ne le connais pas ou que tu n'as pas le droit de l'utiliser, et bien prends

et il existe c entre 0 et 1 tel que:
-\phi(0)=\phi^{'}(c))
en calculant cette dérivée, tu dois tomber sur

Je te remercie déjà, mais je ne sais vraiment comment calculer la dérivée de

-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 01 Sep 2009, 19:36
par ToToR_2000 » 01 Sep 2009, 19:36
Et bien soit tu utilises une formule de dérivation pour ce genre de fonctions à valeurs vectorielles, soit tu la calcules à la main:
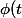=\sum_{i}(b-a)_if_i(a+t(b-a)))
et donc tu dois avoir:
=\sum_{i}(b-a)_i\frac{d(f_i(a+t(b-a)))}{dt}=\sum_{i}(b-a)_i\sum_{k}\frac{\partial f_i(a+t(b-a))}{\partial x_k}\frac{\partial (a_k+t(b_k-a_k)}{\partial t}=\sum_{i}(b-a)_i\sum_{k}\frac{\partial f_i(a+t(b-a))}{\partial x_k}(b_k-a_k))
ce qui est égal au produit scalaire de la différentielle
-
marius1986
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Aoû 2009, 10:33
-
 par marius1986 » 01 Sep 2009, 20:26
par marius1986 » 01 Sep 2009, 20:26
ToToR_2000 a écrit:Et bien soit tu utilises une formule de dérivation pour ce genre de fonctions à valeurs vectorielles, soit tu la calcules à la main:
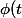=\sum_{i}(b-a)_if_i(a+t(b-a)))
et donc tu dois avoir:
=\sum_{i}(b-a)_i\frac{d(f_i(a+t(b-a)))}{dt}=\sum_{i}(b-a)_i\sum_{k}\frac{\partial f_i(a+t(b-a))}{\partial x_k}\frac{\partial (a_k+t(b_k-a_k)}{\partial t}=\sum_{i}(b-a)_i\sum_{k}\frac{\partial f_i(a+t(b-a))}{\partial x_k}(b_k-a_k))
ce qui est égal au produit scalaire de la différentielle
Je te remercie encore une fois
Mais je pense que tu a utilisé le produit scalaire "classique" pourtant l'on ne spécifie pas de quel produit scalaire il s'agit, en outre tu n'a pas utilisé la deuxième partie de la question (utiliser le théorème des accroissements finis pour la la fonction g)
Merci d'avance
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 02 Sep 2009, 14:08
par ToToR_2000 » 02 Sep 2009, 14:08
Je n'utilise pas le produit scalaire canonique, mais je suppose qu'il existe une base orthonormée dans E et je fais les calculs dedans.
Ceci dit, même avec une base tout court, on pourrait tout de même faire la démonstration.
Quant à g, il ne sert pas dans la démonstration que je te suggère mais on pourrait sans doute l'intégrer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
