Calcul différentiel

[Cornelius]

Bonjour,

Pourriez-vous svp me mettre sur la voie quant à la réponse à cette question :

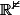
Soit f une application différentiable de dans

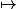
Calculer la dérivée de la fonction : t f(t, f(t,t))

Merci

[Ben314]

Salut,
Si alors
A utiliser deux fois pour conclure.

[barbu23]

Bonsoir, :happy3:

Si je ne m'abuse :
Donc, est une composée de plusieurs fonctions. :happy3:
Donc, il faut que tu appliques la formule :

Cordialement. :happy3:

[zygomatique]

Salut,
Si alors
A utiliser deux fois pour conclure.

salut

j'aurai plutôt écrit ::

Si alors

JFF ... :ptdr:

mais c'est bien sur qu'un détail ....

[Cornelius]

Salut,
Si alors
A utiliser deux fois pour conclure.

Merci mais tu utilises quelle formule ?

[Ben314]

Merci mais tu utilises quelle formule ?

Heuuuu.... je suis pas sur de bien comprendre la question....

Pour faire l'exo, j'utilise la formule que... je t'ai donné dans le post ci dessus.

Si tu me demande quelle formule j'utilise pour démontrer la formule sus-nommée, ben... je suis un peu dans la m... vu que cette formule pour la démontrer, j'utilise pas d'autres formules, mais seulement la définition de ce qu'est une application différentiable...

Je sais pas si je suis clair là :marteau:

[Cornelius]

Heuuuu.... je suis pas sur de bien comprendre la question....

Pour faire l'exo, j'utilise la formule que... je t'ai donné dans le post ci dessus.

Si tu me demande quelle formule j'utilise pour démontrer la formule sus-nommée, ben... je suis un peu dans la m... vu que cette formule pour la démontrer, j'utilise pas d'autres formules, mais seulement la définition de ce qu'est une application différentiable...

Je sais pas si je suis clair là :marteau:

Oui mais commen s'appelle cette formule stp que je puisse lire la démonstration et mieux la retenir par la suite ? J'essaie de devenir un Perelman en relisant toutes les démos quand j'ai le temps.

Je n'arrive pas à faire un lien logique entre le fait que f soit différentiable et cette formule, qui me semble tout droit sortie d'un épisode de Star Trek par translation de 14pi années lumières

[zygomatique]

c'est la formule de la dérivée d'une fonction composée appliquée à une fonction de plusieurs variables ....

[jlb]

Oui mais commen s'appelle cette formule stp que je puisse lire la démonstration et mieux la retenir par la suite ? J'essaie de devenir un Perelman en relisant toutes les démos quand j'ai le temps.

Je n'arrive pas à faire un lien logique entre le fait que f soit différentiable et cette formule, qui me semble tout droit sortie d'un épisode de Star Trek par translation de 14pi années lumières

Tu pourras adapter pour d'autres situations ( traduction matricielle de [fo(u,v)]')