Calcul de déterminant
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 05 Juin 2022, 22:16
par Cezoro » 05 Juin 2022, 22:16
Bonsoir ,
Je ne parvient pas à comprendre le fait suivant:
Pour: (C1,...,Cr) colonnes de M
(Ek) base canonique de Mr+1,r
)
Le coefficient devant t^r est ((-1)^r)*alpha
Le coefficient devant t^(r-1) est
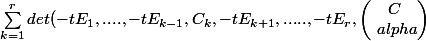)
J'ai essayé de repartir de la définition du déterminant en développant selon une ligne ou une colonne sans succès.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Juin 2022, 22:39
par GaBuZoMeu » 05 Juin 2022, 22:39
Bonsoir,
Pas mal de confusion dans ce que tu écris. Essayons de remettre les choses d'aplomb.
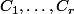
sont des vecteurs colonnes à
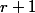
composantes. OK ?
)
est la base canonique de
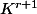
(

le corps de base).

est un vecteur colonne à

composantes,

un scalaire.

est une indéterminée.
)
est une matrice carrée de taille
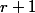
. Son déterminant est un polynôme de degré

en

. Tu obtiens son coefficient dominant et le coefficient de
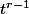
en utilisant la multilinéarité du déterminant par rapport aux colonnes. Tu t'es trompé dans le coeffcient de
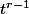
, tu as des

qui ne devraient pas figurer dans ta formule.
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 06 Juin 2022, 12:19
par Cezoro » 06 Juin 2022, 12:19
Merci, je trouve bien les expressions avec la multi linéarité (les t y figurent bien).
J'en profite pour vous demander de l'aide sur la suite où on a l'expression de chaque termes de la somme du coefficient de t^r-1 qui vaut:

Jusqu'ici tout va bien mais je ne parviens pas à comprendre le fait qu'il soit égal à:
^{r-1}t^{r-1}\begin{vmatrix}<br />a_{k,k} &c_{k} \\ <br />l_{k} & alpha<br />\end{vmatrix})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Juin 2022, 22:42
par GaBuZoMeu » 06 Juin 2022, 22:42
Tu te trompes, si tu prends
le coefficient de
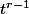
, les

ne figurent pas dans l'expression de ce coefficient ! Les

ont été sortis pour donner le
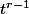
.
Ensuite, il suffit de faire
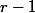
développements suivant les colonnes qui ne contiennent que des 0 et un seul

.
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 13 Juin 2022, 14:13
par Cezoro » 13 Juin 2022, 14:13
Effectivement je m'étais trompé.
C'est plus clair maintenant!
(réponse tardive mais mieux vaut tard que jamais)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
