Calcul de déterminant d'ordre n

[YLS]

Bonjour,

Comment calculer le déterminant suivant :

, où et ?

Avec les opérations pour , j'obtiens une matrice triangulaire avec 2 coefficients par colonne, sauf la 1ère colonne qui est comme celle l'origine, et je ne vois pas quoi en faire...

Merci de votre aide.

[Ben314]

Salut,
Je vois deux méthodes :
1) Tu continue dans cette voie en retranchant la dernière ligne à toutes les autres, puis tu développe par rapport à la premiére colonne : tu obtient deux déterminants (n-1)x(n-1).
Le premier est triangulaire donc immédiat, par contre le deuxième l'est un peu moins mais tu peut trouver sa valeur en faisant une réccurence sur sa taille...

2) Plus astucieuse (mais demandant plus de connaisances) : Il est clair que le déterminant D est un polynôme en a1,a2,...an qui est de degrés 1 par rapport à chacune des variables, c'est à dire que D peut s'écrire alpha_k.ak+beta_k où alpha_k et beta_k ne dépendent pas de ak mais des autres ai (il suffit de voir ce que donnerais le développement par rapport à la k-ième ligne).
De plus, si ak=0 alors en retranchant la k-ième colonne à toutes les autres puis en développant par rapport à la la k-ième ligne on trouve que D=... ce qui donne la valeur du beta_k.
Connaissant tout les beta_k, en réfléchissant un peu, on en déduit quasi complètement le déterminant D (il manque une dernière petite information que l'on peut lire sur le déterminant de départ)

Il y a peut-être d'autres méthodes plus rapides...

[girdav]

Bonjour,
on pourrai écrire le déterminant en question comme la somme de déterminants "hybrides" où l'on prend colonnes de la matrice et de la matrice . On remarque que si l'on prend au moins deux colonnes de , alors le déterminant "hybride" en question est nul puisqu'il y a deux colonnes égales. Il faut donc regarder ce que sont les déterminants où l'on ne prend qu'une colonne de J (il y en a un aussi où l'on n'en prend aucune).

[Ben314]

C'est effectivement... plus rapide !

[YLS]

Salut Ben314 et girdav, merci pour vos réponses.

Pour ta 1ère méthode, Ben314, je trouve bien les deux déterminants annoncés (j'avais complètement oublié qu'on pouvait développer par rapport à une colonne/ligne...), mais le deuxième me semble bien compliqué à calculer...
Ta 2e méthode me plaît plus, moins calculatoire apparemment. Je trouve , par contre je trouve pas le coefficient directeur de chaque fonction affine , en fait je n'arrive pas à faire le lien entre ces écritures affines du déterminant.

girdav, je vois plus ou moins comment tu vas mener tes calculs, mais comment peux-tu décomposer le déterminant comme somme des autres déterminants hybrides? La seule manière que je connaisse d'obtenir une somme de déterminants, c'est de développer, mais là l'ordre des matrices se réduit, ce qui ne semble pas être ta méthode?

[girdav]

Dans le cas général, si on a 2n vecteurs alors en utilisant la linéarité par rapport à la n-ième variable.
On peut continuer le procédé pour les n-1 premières variables de chaque déterminant.

[YLS]

Ok, j'avais pas pensé à ça. En introduisant l'opérateur qui forme une matrice à partir des familles de colonnes données en argument, je trouve une formule de ce genre :



où et désignent respectivement la ème colonne de et .

Quand , le déterminant est nul (au moins 2 colonnes de égales, en effet); si , après développement par rapport à la ème colonne issue de , on a un déterminant égal à , et lorsque , l'unique déterminant vaut alors .

En conclusion, . Exact?


Par contre j'aimerais bien comprendre la méthode polynomiale (cf. là où j'étais rendu avec le message précédent), ça a l'air courant dans le calcul de déterminant. Vous pouvez m'expliquer svp?

[Ben314]

C'est parfaitement ça, et je pense que c'est le plus rapide.

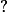
Sinon, ici, la "méthode polynômiale", que je suggérais consiste effectivement à montrer que, pour tout k dans {1..n}, le déterminant est de la forme où ne dépend pas de .
Ensuite, tu attaque "bille en tête" :
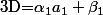
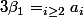
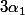
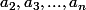
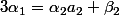
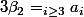
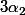
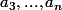
où et est un polynôme en de degrés 1 en chaque variable donc en particulier, il s'écrit où (car en dévelopant, on doit retrouver ) et est un polynôme en de degrés 1 en chaque variable donc... etc

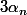
On en déduit qu'en fait où ne dépend de... rien, c'est à dire est une constante.
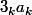
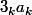
Pour trouver cette constante, on imagine que l'on développe le déterminant à l'aide de la formule "somme pour toute les permutations de Sn du produit..." et on consate que, pour obtenir du il faut prendre tout les termes de la diagonale et que, dans ce cas, le coefficient devant le est le est un 1.

Constatation : c'est nettement plus long que ce qu'a proposé Girdav... (mais c'est rigolo quand même)