Branche infinie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 21:06
par muse » 17 Déc 2006, 21:06
Bonsoir tout le monde
voila j'ai un controle demain sur les branche infinie mais je ne trouve pas d'exercice donc j'aimerai que parmis vous certaine personne me donne des fonction pas trop dur ou je dois trouver la branche infinie.
Je vous remercie infiniement
PS: si vous trouvez un site avec des exos sur les branchnes infinies pas trop dur je prends, j'ai deja chercher en vain :(
merci infiniement
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 21:34
par muse » 17 Déc 2006, 21:34
ha aussi je n'ai pas encore vue les courbe paramétrique
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 21:37
par fahr451 » 17 Déc 2006, 21:37
essaye ça
x-> racine cubique de ( x^3 +x^2 +1)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 21:53
par muse » 17 Déc 2006, 21:53
j'ai calculer le developpement limité au voisinage de l'infinie d'ordre de pour sa j'ai poser X=1/x
je trouve donc
f(x)= 1+
)
je trouve donc que f(x) a une asymptote oblique y=x de plus
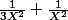
epsilone (X)
est positif donc f est audessus de y=x
vous pouvez confirmer ?
merci bcp bcp bcp
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 21:58
par muse » 17 Déc 2006, 21:58
heu je crois que je me suis planter dans mon raisonnement :s
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:00
par fahr451 » 17 Déc 2006, 22:00
déjà y a + infini et moins infini comme points à regarder
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:03
par muse » 17 Déc 2006, 22:03
en fai j'ai du mal une fois que j'ai fait mon developpement limité avec X je dois faire quoi ? :s
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:05
par fahr451 » 17 Déc 2006, 22:05
écris de nouveau ton dl stp que je puisse contrôler:
f(x) =
et pose plutôt h = 1/x c est plus naturel (un grand X moralement est grand)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:09
par muse » 17 Déc 2006, 22:09
ok a la fin j'obtient:
f(x) = 1+

/2 + x² epsilone (1/x)
mais la je vois pas trop quoi faire

-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:16
par fahr451 » 17 Déc 2006, 22:16
heu
on doit factoriser par l infiniment grand prépondérant ds la racine à savoir x^3
on se limite ds un premier temps à x>0 (on regarde en + inf)
on a f(x) = x racinecubique(1+1/x +1/x^3) on pose 1/x = h
et on fait le dl en 0 de g(h) =(1+h+h^3)^(1/3) à l 'ordre 2 pour avoir à la fin un terme en 1/x qui donnera en effet la position
g(h) = 1 +1/(3h) -1/(9h^2) + 0(h^2)
donc f(x) = x + 1/3 -1/(9x) +(1/x)epsilon(x)
l 'équation de l'asymptote est y = x+1/3 et comme -1/(9x) est égatif la courbe est sous l 'asymptote localement.
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:20
par muse » 17 Déc 2006, 22:20
ben alors la je ne comprends plus rien pourqoui je trouve f(x)= 1+ x²/2 +0(1/x)
et la calculatrice confirme :s
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:22
par fahr451 » 17 Déc 2006, 22:22
quelle expression initiale de f as tu ?
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:25
par muse » 17 Déc 2006, 22:25
racine cubique de 1+x²+x^3
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:25
par muse » 17 Déc 2006, 22:25
mouais c normal je lui ai demander au voisinage de zero :(
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:25
par fahr451 » 17 Déc 2006, 22:25
ben vi j ai la même ; ah oui en zéro c 'est pas pareil... mais on parlerait de tangente non...
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:30
par muse » 17 Déc 2006, 22:30
g(h) = 1 +1/(3h) -1/(9h^2) + 0(h^2)
donc f(x) = x + 1/3 -1/(9x) +(1/x)epsilon(x)
je comprends pas comment tu passe de l'un a l'autre
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:32
par fahr451 » 17 Déc 2006, 22:32
ben y a le x qui est sorti de la racine (ancien x^3) et xh = 1
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:34
par muse » 17 Déc 2006, 22:34
hum je ne comprends pas :(
si prend g et que tu remplace h et apres tu multiplie tout par x (ancien x^3) sa te donne pas ce que tu as mis :s
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Déc 2006, 22:37
par fahr451 » 17 Déc 2006, 22:37
tu es d 'accord que f(x) = x g(h) avec h = 1/x ; h infiniment petit ?
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 17 Déc 2006, 22:42
par muse » 17 Déc 2006, 22:42
oui je suis daccord
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
