Branche et Coupure

[sky-mars]

Bonjour tout le monde ! :)

Je comprends pas trés bien la notion de branchement et de coupure ? Pourrai t on m'expliquer ça avec un (ou des) simple(s) exemple(s) s'il vous plait ? ?

[Arkhnor]

Salut.

Bien que tout nombre complexe non nul puisse s'écrire sous la forme exp(z), on ne peut définir sur C privé de 0 une fonction Log continue telle que exp(Log z) = z pour tout z.

Si U est un ouvert simplement connexe de C\{0}, alors il existe une application Log analytique sur U, et vérifiant exp o Log = Id. (il en existe une infinité, elles différent d'un multiple de 2iPI)

Une manière de construire un ouvert simplement connexe de C\{0} est de retirer une demi-droite issue de 0. (c'est ce qu'on appelle une coupure)

On rencontre le même problème avec la racine carrée, et plus généralement les fonctions puissances non entières (que l'on peut définir avec la fonction Log).

La notion de point de branchement provient essentiellement des surfaces de Riemann, je ne peux pas beaucoup t'en dire plus.

[sky-mars]

tout d'abord de cette réponse, pourrais tu m'illustrer ce que tu m'as dit avec un exemple simple ?

admettons si j'ai f ( z ) = (z - 1) ^(1/3) , qu'est ce tu ferai ?

[Arkhnor]

Tout d'abord, choisir un domaine simplement connexe et une détermination du logarithme. Ensuite, se rappeler que l'on définit . Et déterminer le domaine de définition de ta fonction (ici, les z tels que Log(z-1) soit défini).

[sky-mars]

donc ici z € ] 1, +OO[ notre fonction est définie et c'est là qu'on place la coupure ?

[sky-mars]

et ici qu'est ce qu'on appelle détermination ? ??

[Arkhnor]

Oui, tu peux choisir la coupure comme étant 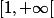(tu aurais bien sur pu en choisir une autre, comme )

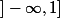Ta fonction est donc défini sur le complémentaire de cette coupure. (tu dois quand même préciser la définition du logarithme que tu choisis, car comme je te l'ai dit, sur un ouvert simplement connexe, il existe une infinité de déterminations du logarithme qui différent d'une constante)

Tu peux par exemple calculer la dérivée de cette fonction.

[Arkhnor]

Une détermination du logarithme, c'est le choix d'un domaine et d'un logarithme sur ce domaine.

[sky-mars]

il existe pas de meilleur coupure ? vue qu'il en existe une infinité
Mais je comprends pas pourquoi tu peux prendre ]-OO ; -1 [ ? (log complexe définie sur C* ? )
Comment tu fais pour déterminer le nombre de détermination ?

[sky-mars]

ah okey donc ici sa serait 2 détermination puisqu'on a dit qu'on pouvait faire une coupure soit sur ]-1, +OO [ ou ]-OO , -1 [

[Arkhnor]

N'importe quelle demi-droite issue de 1 convient, et pour chaque domaine correspondant, il existe une infinité de logarithme, donc il n'y a pas que 2 déterminations !

Dans les applications, on en choisit juste une qui nous parait naturelle : on choisit une coupure, et ensuite on choisit un logarithme.
Le choix peut-être guidé par la nature de l'opération que l'on veut effectuer ...

Exemple :

On choisit D = C\R+, l'application , où 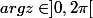et k un entier relatif quelconque, est une détermination du logarithme sur D.
On aurait pu prendre D = C\R-, et et prendre l'argument à valeur dans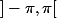 , ou encore D = C\iR+ (C privé d'une demi droite verticale vers le haut) et l'argument à valeur dans 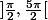, etc ...

Si tu cherches à définir toutes les déterminations de ta fonction, tu as une infinité de choix de domaine, et une fois le domaine fixé, plusieurs choix de déterminations. (éventuellement une infinité, comme pour le logarithme)

[Arkhnor]

J'ai peut-être mal interprété ton dernier message, ce sont effectivement 2 déterminations du logarithme. (mais ce ne sont pas les seules)

[Arkhnor]

Comme on définit l'expression par , z doit être tel que Log(z-1) soit défini.

Si on choisit une détermination du log définie sur C\R+, z-1 ne doit pas appartenir à R+, c'est à dire que z ne doit pas être un réel supérieur ou égal à 1.

Si la coupure du log est R-, z ne doit pas être un réel inférieur ou égal à 1.

[sky-mars]

ah okey ! et sa sert à rendre les fonctions multiformes uniformes c'est ca ?

[Arkhnor]

Qu'entend tu exactement par là ?

(Je n'aime pas trop les termes uniformes/multiformes car formellement, une fonction ne peut prendre qu'une seule valeur en un point, et dire qu'une fonction prend plusieurs valeurs en un point est une absurdité ...)

[sky-mars]

une fonction uniforme c'est si on a z = z ' alors f ( z ) = f ( z' )
et multiforme c'est si on a z = z ' alors f ( z ) =! f (z' ) non ?

[Arkhnor]

Attention, le point 1 est compris dans la coupure ! Les déterminations de (z-1)^(1/3) n'est pas définie en 1. (c'est le fameux point de branchement)

[Arkhnor]

Comme je te l'ai dit, la notion de fonction multiforme (telle que tu me la donnes) est une absurdité. Si on t'as présenté les choses de cette façon, c'est par simplicité, mais c'est tout sauf satisfaisant.

En effet, si f prend 2 valeurs différentes en z, que peut-on dire de la quantité f(z) + f(z) ? Est-ce que c'est 2 fois la première valeur ? 2 fois la seconde ? La première plus la seconde ?
Et ça empire pour f(z) + f(z) + f(z) ...

[sky-mars]

ah en effet c'est assez ambigu ! (lol vive la rigueur des maths en école d'ingénieur :p )
Mais si par exemple, on définit notre domaine et la coupure l'ambiguité se dissipe non ?

[Arkhnor]

Oui, car ce que l'on définit depuis le début de ce message, ce sont de "vraies" fonctions (uniformes si tu préfères) qui ne prennent qu'une seule valeur en un point.

C'est juste que l'on a plusieurs choix possibles, mais une fois le choix effectué, on a qu'une seule fonction, et une seule valeur en chaque point.