Arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 09 Avr 2013, 12:54
par Zix » 09 Avr 2013, 12:54
bonjour j'ai deux petits exercices à faire et j'aurais besoin d'aide.
Ex1 : Pour quelle valeur de la constante a le polynôme "P(X) = (X+1)^3 - X^3 - a" possède une racine double
Ex2 : a) Démontrer que (X^2 - 1)^2 + (2X)^2 = (X^2 +1)^2
b) Remplacer X par p/q avec p et q entiers, puis réduire au même dénominateur . En déduire qu'il existe une infinité de triplets d'entiers non (a,b,c) tels que a^2 + b^2 = c^2
pour l'ex1 comment faut-il procéder ? et pour le 2) c'est la question b) que je ne comprends pas.
Merci d'avance
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Avr 2013, 13:03
par arnaud32 » 09 Avr 2013, 13:03
1/si r est racine double P(r)=P'(r)=0 ...
2a/ a²+b²=a²-(ib)²=(a+ib)(a-ib) ...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Avr 2013, 13:37
par chan79 » 09 Avr 2013, 13:37
Pour la 1, en développant, les x³ disparaissent. On peut écrire que le discriminant est nul.
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 09 Avr 2013, 15:05
par Zix » 09 Avr 2013, 15:05
chan79 a écrit:Pour la 1, en développant, les x³ disparaissent. On peut écrire que le discriminant est nul.
J'ai trouvé a = 1/4, c'est bon ?
arnaud32 a écrit:2a/ a²+b²=a²-(ib)²=(a+ib)(a-ib) ...
L'indice que tu m'as donné c'est pour la question a) ou b) ? Car j'ai dejà fait la question a)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Avr 2013, 15:59
par arnaud32 » 09 Avr 2013, 15:59
a=1/4 c'est bon
c'etait pour la 2a
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 09 Avr 2013, 16:40
par Zix » 09 Avr 2013, 16:40
arnaud32 a écrit:a=1/4 c'est bon
c'etait pour la 2a
Ok si c'est le cas, j'aimerais un peu d'aide pour la question b), déjà, je remplace X par p/q dans quelle équation et la notion d'existence d'infinité de triplets, ça me parait confus
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 09 Avr 2013, 17:20
par Archibald » 09 Avr 2013, 17:20
L'énoncé te dit
En déduire qu'il existe une infinité de triplets d'entiers non (a,b,c) tels que a^2 + b^2 = c^2
Donc tu poses
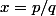
et remplace dans
^2 + ({2x})^2 = ({x^2+1})^2)
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 09 Avr 2013, 18:58
par Zix » 09 Avr 2013, 18:58
Archibald a écrit:L'énoncé te dit
Donc tu poses
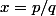
et remplace dans
^2 + ({2x})^2 = ({x^2+1})^2)
On a ((p^2 - q^2)/q^2)^2 - (2p/q)^2 = ((p^2 + q^2)/q^2)¨2. Mais...quelle relation je dois trouver ou retrouver ? je comprends pas.
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 09 Avr 2013, 20:16
par Archibald » 09 Avr 2013, 20:16
Attention, c'est
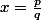
et non pas
 = \frac{p}{q})
^2+(2\frac{p}{q})^2=(\frac{p^2}{q^2}+1)^2)
Il ne te reste plus qu'à développer puis réduire l'expression au même dénominateur.
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 09 Avr 2013, 21:41
par Zix » 09 Avr 2013, 21:41
je trouve (p^4 + 2p^2.q^2 + q^2)/q^4, ça justifie à lui seul la question ?
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 10 Avr 2013, 10:51
par Archibald » 10 Avr 2013, 10:51
^2 \quad + \quad (2\frac{p}{q})^2 \quad = \quad (\frac{p^2}{q^2}+1)^2 \quad \longleftrightarrow \quad (\frac{p^4}{q^4}+1-2 \frac{p^2}{q^2}) \quad + \quad 4\frac{p^2}{q^2} \quad = \quad (\frac{p^4}{q^4}+1 + 2 \frac{p^2}{q^2}) \quad \longleftrightarrow)
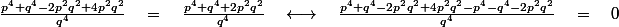
Etc....
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 10 Avr 2013, 11:27
par Zix » 10 Avr 2013, 11:27
l'égalité de gauche fait 0,voilà.. mais ça justifie quoi ?
Sinon j'ai trouvé une autre justification sur internet :
Soit (x;y;z) un triplet pythagoricien alors x²+y²=z²
on a:
qq soit n élément de IN*: n²x²+y²n²=z²n²
donc (nx;ny;nz) est un triplet pythagoricien
donc il y a une infinité de triplets pythagoriciens

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Avr 2013, 11:28
par chan79 » 10 Avr 2013, 11:28
^2+(2\frac{p}{q})^2=(\frac{p^2}{q^2}+1)^2)
en mettant tout sur
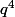
et en multipliant les deux membres par
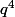
, on obtient
^2+(2pq)^2=(p^2+q^2)^2)
par exemple pour p=7 et q=5, cela donne 24²+70²=74²
en gardant q=5 et en augmentant p, on fait apparaître une infinité de solutions:
p=7 donne 24²+70²=74²
p=8 donne 39²+80²=89²
p=9 donne 56²+90²=106²
p=10 donne 75²+100²=125²
...
...
...
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 10 Avr 2013, 11:45
par Archibald » 10 Avr 2013, 11:45
Zix a écrit:l'égalité de gauche fait 0,voilà.. mais ça justifie quoi ?

infinité de solutions !
Autrement dit, il existe une infinité de triplets qui vérifie cette égalité.
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 10 Avr 2013, 12:48
par Zix » 10 Avr 2013, 12:48
Archibald a écrit:
infinité de solutions !
Autrement dit, il existe une infinité de triplets qui vérifie cette égalité.
Très bien merci à vous pour votre aide et bonne journée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 116 invités
