Action sur un groupe différentiel.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 18:51
par Finrod » 01 Fév 2010, 18:51
Voilà une des dernière questions que j'ai cherché.
Soit G un groupe différentiel commutatif, on note d sa différentielle.
Alors
)
agit sur G par n.g =
}(g))
(la dérivée n-ème).
Or

agit aussi sur G par multiplication : z.g = zg
Montrer que si un groupe (ou un monoïde) contenant

et

agit sur G et relève les deux actions, alors il agit trivialement sur G (i.e. par Id) .
AUtrement dit les deux actions sont totalement incompatibles : en voyez vous la raison ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 19:01
par Ben314 » 01 Fév 2010, 19:01
Salut,
Comme j'ai jamais vu la notion de groupe différentiel, peut tu me donner la définition ?
[Pour moi une dérivation, ça doit vérifier d(a+b)=d(a)+d(b) et d(a.b)=d(a).b+a.d(b) mais il faut au mini être dans un anneau... ou alors tu parle de groupes de lie...]
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 19:05
par Finrod » 01 Fév 2010, 19:05
Le groupe est muni d'une action additive ici donc la différentielle est juste un endomorphisme de groupe.
Le fait que G est ou non une autre loi, multiplicative n'intervient pas.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 19:14
par Ben314 » 01 Fév 2010, 19:14
Résumé : G est un groupe commutatif (je le suppose vu ta notation
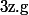
qu tu aurais noté sinon
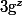
... ) et d un morphisme de groupe de G dans G.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Fév 2010, 19:24
par Doraki » 01 Fév 2010, 19:24
Si G n'était pas commutatif la multiplication ne serait pas une action.
Tu veux dire quoi par "relever une action" ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 19:25
par Finrod » 01 Fév 2010, 19:25
Oui en fait dans le cas que j'éai étudié l'endomorphisme qui correspondait à l'action de

était la différentielle mais tel que j'ai posé l'exo cette information est superflue.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 19:27
par Finrod » 01 Fév 2010, 19:27
Je veux dire que par la composition
 \rightarrow H \rightarrow G)
redonne l'action de N et de Z à partir de l'action de H.
ou H est le truc auquel je n'ai pas donné de nom plus haut.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 19:37
par Ben314 » 01 Fév 2010, 19:37
H est sensé être commutatif ?
Sinon, j'ai l'impression qu'en prenant le produit libre (au sens monoïdes non commutatifs) je vois pas trop quelle obstruction on peut avoir...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Fév 2010, 19:41
par Doraki » 01 Fév 2010, 19:41
Donc alors en fait,
je prends G quelconque,
je prends H = (Z,*), avec l'action de multiplication,
je prends d = la multiplication par un nombre au hasard y.
(N,+) est bien sur contenu dans (Z,*) via x -> y^x,
Alors je dois montrer que pour tout z de Z et g de G, z.g = g ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 19:41
par Ben314 » 01 Fév 2010, 19:41
Doraki a écrit:Si G n'était pas commutatif la multiplication ne serait pas une action.
Là, il y a un truc qui m'échappe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Fév 2010, 19:45
par Doraki » 01 Fév 2010, 19:45
Ah ben oui t'as raison j'avais une définition étrange d'action.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 20:01
par Finrod » 01 Fév 2010, 20:01
C'est de l'algèbre commutative, tout est commutatif.
@Doraki> quand je disais trivial, en fait c'est action nulle ici z.g = 0 pour tout g. (j'avais dit action Id mais j'avais pas revérifier, c'était un chance sur 2)
Le but de l'exo est juste de bien comprendre certains formalismes. J'en ai eu en tout besoin.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Fév 2010, 20:10
par Doraki » 01 Fév 2010, 20:10
Savoir que je dois montrer que 2*3 = 0 à la place de 2*3 = 3 ne me rassure pas tellement.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 20:14
par Ben314 » 01 Fév 2010, 20:14
Y'a (encore) un truc qui m'échappe :
Finrod a écrit:...c'est action nulle ici z.g = 0 pour tout g...
Ton action, elle est pas sensé prolonger l'action de Z sur G ? (je veut bien qu'elle prolonge l'action de N* dans le cas où d=0...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Fév 2010, 20:19
par Ben314 » 01 Fév 2010, 20:19
Un dernier (?) truc que je pige pas :
l'action de Z par multiplication (m.g=mg) c'est à la fois une action du groupe (Z,+) et aussi du monoïde (Z,x) et jusque là, on s'en fout de savoir lequel des deux agit.
MAIS, lorsqu'il dit que H "contient" Z, je pense que ça signifie qu'il existe un morphisme injectif de Z dans H et là, il faudrait savoir si le morphisme c'est de (Z,+) dans H ou de (Z,x) dans H (à priori, on n'a qu'une seule opération dans H)...
P.S. Je pencherais pour (Z,+)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 20:24
par Finrod » 01 Fév 2010, 20:24
La difficulté de la preuve vient du fait que notre intuition est parfois en contradiction avec certain formalismes.
Dans ton exemple (Z), ça donne bien une action nulle.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 20:25
par Finrod » 01 Fév 2010, 20:25
Ben314 a écrit:Y'a (encore) un truc qui m'échappe :
Ton action, elle est pas sensé prolonger l'action de Z sur G ? (je veut bien qu'elle prolonge l'action de N* dans le cas où d=0...)
Oui c'est absurde donc on conclut qu'un tel objet prolongeant les actions n'existe pas.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 20:27
par Finrod » 01 Fév 2010, 20:27
Ben314 a écrit:Un dernier (?) truc que je pige pas :
l'action de Z par multiplication (m.g=mg) c'est à la fois une action du groupe (Z,+) et aussi du monoïde (Z,x) et jusque là, on s'en fout de savoir lequel des deux agit.
MAIS, lorsqu'il dit que H "contient" Z, je pense que ça signifie qu'il existe un morphisme injectif de Z dans H et là, il faudrait savoir si le morphisme c'est de (Z,+) dans H ou de (Z,x) dans H (à priori, on n'a qu'une seule opération dans H)...
P.S. Je pencherais pour (Z,+)...
Oui mais si tu prends (Z,+) ça marche bien.
Il y a problème avec (Z, .)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 01 Fév 2010, 20:36
par Finrod » 01 Fév 2010, 20:36
Par acquis de conscience, j'ai vérifié.
Donc l'action composé avec N devient nulle, sauf en zéro ou elle vaut l'identité. (on y peut rien)
En fait on montrer que le morphisme de N dans H est nul, sauf en zéro où il envoi sur 1.
Du coup, l'action composé avec Z n'a pas de raison d'être touchée. Je me suis mal exprimé. (H,.) agit bien sur G.
J'ai voulut reformuler la question originale, qui était de montrer que H ne pouvait exister, avec des détails, et j'y ai été un peu fort ^^.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Fév 2010, 20:37
par Doraki » 01 Fév 2010, 20:37
euh depuis quand la multiplication est une action de (Z,+) et pas de (Z,*) ?
je veux bien mais alors ça veut dire que pour tout g, 0.g = g = e.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités