Bonjour !
Voici un exercice sur une petite application d'action de groupe.
Soient
un groupe
fini de
)
(groupe des rotations) et
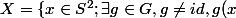=x\} \subset S^{2})
où
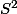
est la sphère unité de
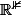
avec la norme euclidienne.
1) a. Montrer que agit sur 
.Bon alors ça, j'ai défini une action
=g(x))
.
Si
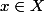
, comme la rotation est une isométrie on a déjà
 ||=1)
. De plus
=x)
=>
=g(x)=g_1g(x))
donc
 \in X)
.
On en déduit que
est bien définie.
Ensuite on a les propriétés
=id(x)=x)
et
=\phi(g,\phi(g_1,x)))
.
est donc une action de G sur X...
b.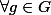 
, déterminer Card()
).Si
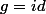
alors
=\{x \in X; id(x)=x\}=X)
Si
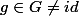
alors
=\{x \in X; g(x)=x\})
,
si on note
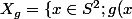=x\})
alors on a
=X_g)
... Mais je vois pas plus ce qu'on pourrait faire, ni comment déterminer les cardinaux.
Je mettrai la suite de l'énoncé au fur et à mesure, si quelqu'un a la patience de bien vouloir m'éclairer.
Merci ^^
