Action de groupe, action fidèle...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Invaders
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Fév 2012, 22:40
-
 par Invaders » 07 Nov 2012, 20:19
par Invaders » 07 Nov 2012, 20:19
Bonjour !
Voici le problème :
Soit :
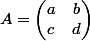
)
 + b}{c (-\frac dc) + d} = \infty)
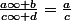
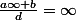
lorsque c=0
1 - montrer que l'application
)
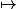
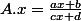
définit une action de
)
sur
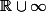
2 - montrer que cette action :
- n'est pas fidèle, décrire son noyau
- est transitive
- est 2-transitive
3 - montrer que la formule définit une action de
)
sur
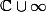
, déterminer les orbites de cette action
Je suis rendue à la question 2, au calcul du noyau. Je trouve que le noyau est égal à +/- Id.
je voulais savoir si mon résultat était correct.
Et si vous avez des pistes pour les autres questions (2 et 3) je suis preneur !
Merci beaucoup !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 08 Nov 2012, 11:52
par cuati » 08 Nov 2012, 11:52
Bonjour.
Pour le noyau je confirme ta réponse.
Pour la transitivité tu peux montrer par exemple (quitte à composer par des inverses de matrices par la suite) montrer que pour tout
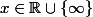
il existe
)
tel que
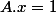
, en discutant les cas
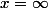
ou non. On peut appliquer la même méthode pour la 2-transitivité : montrer par exemple que pour tout
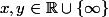
il existe
)
tel que
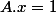
et
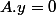
par exemple... mais là encore il faut discuter (couper des cheveux en 4) selon certaines valeurs particulières...
-
Collap35
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Déc 2011, 19:42
-
 par Collap35 » 08 Nov 2012, 20:12
par Collap35 » 08 Nov 2012, 20:12
Bonjour,
J'ai le même exercice à faire, ce qui me pose problème c'est la 2-transitivité. Pour montrer que l'action de SL(2,R) sur RU{infini} est 2-transitive, serait-il équivalent de montrer que l'action de SL(2,R) sur (RU{infini})^2 définie par : A.(x,y)=(A.x , A.y) est transitive ? (en montrant par exemple que l'orbite de (1,1) est égale à (RU{infini})^2)
Merci pour vos réponses ! :)
-
Invaders
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Fév 2012, 22:40
-
 par Invaders » 08 Nov 2012, 20:57
par Invaders » 08 Nov 2012, 20:57
cuati a écrit:Bonjour.
Pour le noyau je confirme ta réponse.
Pour la transitivité tu peux montrer par exemple (quitte à composer par des inverses de matrices par la suite) montrer que pour tout
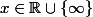
il existe
)
tel que
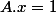
, en discutant les cas
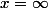
ou non.
Merci beaucoup pour votre aide.
Mais je pense avoir un problème car j'aboutis à une contradiction.
Je m'explique, je pars de l'égalité
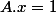
, on distingue donc 2 cas :
cas où
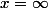
, on a
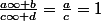
, d'où

cas où
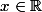
, on a
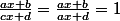
d'où
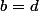
Ensuite je me sers du fait que
)
, j'ai donc, ad - bc = ad - da = 1 = 0 !!!!
Je ne sais pas où est mon erreur :s
Merci pour votre aide.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 08 Nov 2012, 21:39
par cuati » 08 Nov 2012, 21:39
Ne mélange pas les deux cas, la transitivité, ici, c'est : pour tout x il existe A tel que...
Le A n'est donc pas nécessairement le même pour
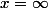
et
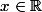
(il n'y a d'ailleurs aucune raison pour que cela soit le même A). En fait les coefficients de A dépendent de x !
-
Invaders
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Fév 2012, 22:40
-
 par Invaders » 08 Nov 2012, 22:31
par Invaders » 08 Nov 2012, 22:31
Ahhhhh ok, je n'avais pas du tout compris ça !
Du coup pour
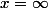
on a
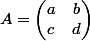
avec a=c
et pour
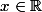
on a
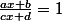
d'où
 = (cx + d))
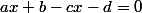
 + (b - d) = 0)
je distingue ensuite tous les différents cas ?
Merci par avance !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 09 Nov 2012, 21:59
par cuati » 09 Nov 2012, 21:59
Désolé pour le retard (j'ai peu de temps disponible).
Enfin voilà faisons le avec 0 :
Si
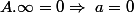
et alors
\Leftrightarrow\;bc=-1)
. Il y a alors une infinité de choix possibles pour b,c,d.
Si
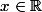
alors
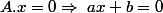
donc
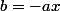
et alors
\Leftrightarrow\;ad+cax=1)
. Il suffit donc de prendre
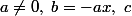
quelconque et
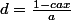
. Là encore on a une infinité de choix possibles pour a,b,c,d.
Dans tous les cas, on a montré que pour tout
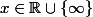
il existe
)
tel que
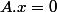
. Soit donc deux éléments

et

de
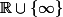
et soit encore

et

deux éléments de
)
tels que
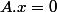
et
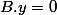
. On a alors
)
et
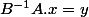
. Ce qui prouve bien de l'action est transitive.
-
Collap35
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Déc 2011, 19:42
-
 par Collap35 » 13 Nov 2012, 21:07
par Collap35 » 13 Nov 2012, 21:07
Bonsoir,
J'essaye de montrer que l'action de SL(2,R) sur RU{infini} est 2-transitive avec la même méthode, c'est-à-dire : pour tout couple (x,y) de RU{infini}^2 il existe A dans SL(2,R) telle que (A.x , A.y)=(0,0). Malheureusement j'aboutis à une contradiction dans le cas où x=infini et y un réel, en effet :
A.infini=0 implique que a/c=0 soit a=0
et A.y=0 implique que ay=-b
Donc on doit avoir a=b=0, mais alors det(A)=ad-bc=0, donc A n'appartient pas à SL(2,R) !
Où ai-je fait une erreur ? Merci d'avance pour votre aide !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Nov 2012, 21:33
par cuati » 13 Nov 2012, 21:33
Bonsoir,
tu peux revoir la définition de la 2-transitivité, les éléments doivent être distincts, tu ne peux donc pas choisir (0,0). Essaye avec
)
par exemple...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
