6122 résultats trouvés
Revenir à la recherche avancée
Re: DM maths 1ère (dérivation, exponentielle, signe, variati
1. g est dérivable en tant que somme sur R. de fonctions dérivables sur R Sa dérivée est g’(x)=1+e^x -1+e^x 2. g(x)=1-x+e^x g(0)=1-0+e^0 g(0)=-1-0+1 1-0+1 4. f est du signe de g(x) car e^-x est toujours positif. f' est du signe de g(x) Ainsi, f est décroissant entre -oo et x=0 Non 6. Etudie le sign...
- 26 Avr 2022, 20:13
- Forum: ✎✎ Lycée
- Sujet: DM maths 1ère (dérivation, exponentielle, signe, variation)
- Réponses: 1
- Vues: 577
Re: Question trigonométrie
Es-tu certaine de l'équation de départ ?
- 24 Avr 2022, 14:02
- Forum: ✎✎ Lycée
- Sujet: Question trigonométrie
- Réponses: 4
- Vues: 264
Re: Question trigonométrie
Si tu poses X = cos x, tu obtiens une équation du second degré que, je suppose, tu sais résoudre
- 24 Avr 2022, 13:46
- Forum: ✎✎ Lycée
- Sujet: Question trigonométrie
- Réponses: 4
- Vues: 264
Re: equation cartesienne dans repere orthonormé coordonnées
C'est donc que tu n'as pas compris ce qu'est une équation cartésienne de droite. Prenons D: 13x - 4y = 0. Les coordonnées de tous les points M(x,y) de D sont reliées par 13x-4y=0. Pour tracer la droite, il suffit d'en déterminer 2 points distincts. Pour x=4 par exemple, y=13 * 4/4 = 13 donc le point...
- 23 Avr 2022, 15:36
- Forum: ✎✎ Lycée
- Sujet: equation cartesienne dans repere orthonormé coordonnées
- Réponses: 1
- Vues: 286
Re: Intégrale par la méthode des trapèzes.
C'est bon pour la méthode mais le calcul final est faux
- 22 Avr 2022, 20:14
- Forum: ✯✎ Supérieur
- Sujet: Intégrale par la méthode des trapèzes.
- Réponses: 6
- Vues: 352
Re: Présentation
Bienvenue à toi !
- 21 Avr 2022, 18:27
- Forum: ✌ Présentez-vous
- Sujet: Présentation
- Réponses: 1
- Vues: 4818
Re: Produits Scalaires
Pour la 1, c'est OK mais tu pouvais faire plus simple
MI.BH = MI.(BA+AH) = MI.BA + MI.AH = MI.AH
Oui IA = -IB
BH.(MH+MI) = BH.MH + BH.MI = MH.HA (par 2) + MI.AH (par 1) = MH.HA + IM.HA = IH.HA = 0
MI.BH = MI.(BA+AH) = MI.BA + MI.AH = MI.AH
Oui IA = -IB
BH.(MH+MI) = BH.MH + BH.MI = MH.HA (par 2) + MI.AH (par 1) = MH.HA + IM.HA = IH.HA = 0
- 14 Avr 2022, 20:27
- Forum: ✎✎ Lycée
- Sujet: Produits Scalaires
- Réponses: 9
- Vues: 494
Re: Question au sujet d'un ancien membre très actif
Je t'ai répondu en MP.
- 14 Avr 2022, 20:12
- Forum: ⚑ À propos de ce site
- Sujet: Question au sujet d'un ancien membre très actif
- Réponses: 3
- Vues: 1943
- 12 Avr 2022, 20:35
- Forum: ✎ Collège et Primaire
- Sujet: a l`aide
- Réponses: 4
- Vues: 750
Re: enigme
Mon conseil : faire un dessin
- 27 Mar 2022, 17:43
- Forum: ⚔ Défis et énigmes
- Sujet: enigme
- Réponses: 2
- Vues: 320
Re: DEVOIR MAISON
anos99 est un bot
- 27 Mar 2022, 13:16
- Forum: ✎ Collège et Primaire
- Sujet: DEVOIR MAISON
- Réponses: 8
- Vues: 801
Re: Equation du second degré
J'ai fusionné les posts pour la compréhension globale
- 25 Mar 2022, 18:56
- Forum: ✎✎ Lycée
- Sujet: Equation du second degré
- Réponses: 10
- Vues: 528
- 13 Mar 2022, 21:22
- Forum: ✯✎ Supérieur
- Sujet: • Calcul d'une intégrale •
- Réponses: 2
- Vues: 360
Re: Matrice
On suppose que 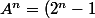 A + \left(2-2^n \right) I)
On multiplie par A et on utilise le fait que A² = 3A - 2I
On multiplie par A et on utilise le fait que A² = 3A - 2I
Re: Matrice
Neptunefaitdesmaths a écrit:J'ai bien réussi les 2 premières questions mais je suis bloqué à la 3.
Pouvez-vous m'aider ?
La récurrence
Re: [URGENT!] Vecteur et parallélisme
EX1 ABC est un triangle. E et F sont les points tels que : (vecteur) AE = 1/3 (vecteur)AB et (vecteur)CF =2/3 (vecteur)CA. Les droites (EF) et (BC) sont-elles parallèles? Justifier. Je suppose que tu as vu la relation de Chasles ? Essaie d'exprimer \vec{EF} en fonction de \vec{BC} en décomposant \v...
- 13 Mar 2022, 14:45
- Forum: ✎✎ Lycée
- Sujet: [URGENT!] Vecteur et parallélisme
- Réponses: 10
- Vues: 478
Re: olympiade
En dehors des règles classiques du type : si la somme des chiffres d'un nombre est divisible par 3, alors ce nombre est divisible par 3, tu peux tester la division de 2021 par les nombres premiers jusqu'à 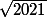
- 21 Fév 2022, 18:34
- Forum: ⚜ Salon Mathématique
- Sujet: olympiade
- Réponses: 2
- Vues: 362
Re: Bonjour
Bienvenue Julien !
- 20 Fév 2022, 21:41
- Forum: ✌ Présentez-vous
- Sujet: Bonjour
- Réponses: 4
- Vues: 766
Re: Problème de Maths
En combien de temps le 1er cycliste arrive-t-il au point B ?
C'est la durée de vol de la mouche, qui va à 25 km/h.
C'est la durée de vol de la mouche, qui va à 25 km/h.
- 19 Fév 2022, 18:16
- Forum: ✎✎ Lycée
- Sujet: Problème de Maths
- Réponses: 1
- Vues: 295
Re: Logarithmes
Ben c'est un peu la définition du logarithme, non ?
Cf. wikipedia "En mathématiques, le logarithme de base b d'un nombre réel strictement positif est la puissance à laquelle il faut élever la base b pour obtenir ce nombre."
Cf. wikipedia "En mathématiques, le logarithme de base b d'un nombre réel strictement positif est la puissance à laquelle il faut élever la base b pour obtenir ce nombre."
- 09 Fév 2022, 20:37
- Forum: ✌ Présentez-vous
- Sujet: Logarithmes
- Réponses: 2
- Vues: 498
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
