Une integral qui me donne la migraine...

[SkyPixell]

Bonjour tout le monde,

Je veux savoir comment résoudre cette integrale d'une méthode théorique ( pas graphique ). J'ai passé plus de 3 jours à essayer de la résoudre mais en vain. Merci davantage pour votre soutien.

∫ √(1+tan(x)+tan²(x)) de 0 vers pi/4

[Rdvn]

Bonsoir
faire le changement de variable
t=tan(x)
valide pour x variant dans
] -Pi/2 , Pi/2 [
proposez vos essais

[SkyPixell]

Cela n'a rien donné.. je l'avais déjà essayé 2 jours auparavant...

[Rdvn]

En effet, il me semble à présent qu'il y a une racine carrée pour la fonction à intégrer :
je ne l'avais pas vue tout à l'heure
Est ce cela ?

[SkyPixell]

Oui il y a une racine!

[Rdvn]

Ça me parait beaucoup plus compliqué .
Je n'ai plus le temps de chercher : je passe mon tour au profit d'un autre membre du forum
plus inspiré et/ou plus disponible
Bon courage

[SkyPixell]

Ça me parait beaucoup plus compliqué .
Je n'ai plus le temps de chercher : je passe mon tour au profit d'un autre membre du forum
plus inspiré et/ou plus disponible
Bon courage

Merci en tout cas!!

[Black Jack]

Bonjour,

Changement de variables : tan(x) = t amène à

2 ème changement de variables :

cela amène : t = (u²-1)/(1-2u)
dt = -2(u²-u-1)/(1-2u)² du
1+t² = (u^4 + 2u²-4u+2)/(1-2u)²
t = 0 --> u = 1 et t = 1 --> u = RacineCarrée(3) - 1

Et l'intégrale devient après simplifications :



Qui devrait pouvoir être calculé par des méthodes classiques ... puisque c'est une "simple" fraction rationnelle.

Mais je n'ai pas le courage de poursuivre.

Mon singe donne I = 1,01559 (arrondi)

[Black Jack]

Bonjour,

Dans ma grande mansuétude je vais une étape plus loin ...

(u-u²-1)²/[(1-2u)(u^4+2u²-4u+2)]
=(u^4-2u³+3u²-2u+1)[(1-2u).(u²-V2.u+2-V2).(u²+V2.u+2+V2)] (avec V pour racine carrée)

Que l'on peut décomposer ainsi : = A/(1-2u) + (Bu+c)/(u²-V2.u+2-V2) + (Du+E)/(u²+V2.u+2+V2)

Qui donne A(u^4+2u²-4u+2) + (Bu+c).(1-2u).(u²+V2.u+2+V2) + (Du+E).(1-2u).((u²-V2.u+2-V2) = u^4-2u³+3u²-2u+1

On identifiant les coefficients de même puissance de u des 2 membres, on a 5 équations à 5 inconnues qui résolu donne :

A = 1
B = 0,353553390593
C = -0,353553390593
D = -0,353553390593
D = -0,353553390593

Et donc (u-u²-1)²/[(1-2u)(u^4+2u²-4u+2)] = 1/(1-2u) + 0,353553390593 * (u-1)/(u²-V2.u + 2-V2) - 0,353553390593 * (u-1)/(u²+V2.u + 2+V2)

Qui est tout à fait basique à intégrer ...

[catamat]

Bonjour

Bien vu Black jack

Juste une remarque
La valeur exacte de B, C, D et E est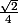

et une petite coquille (qui prouve que j'ai lu avec attention et intérêt !) au début c'est :
dt = -2(u²-u+1)/(1-2u)² du
mais c'est corrigé par la suite