322 résultats trouvés
Revenir à la recherche avancée
Bonjour ,
Pourquoi les vagues sont-elles si destructrices sur la côte uniquement ?
C'est une question d'énergie et de profondeur non ?
merci
- par ptitemimidu18
- 10 Sep 2008, 19:06
-
- Forum: ⚛ Physique
- Sujet: les vagues
- Réponses: 4
- Vues: 530
j'ai lu le document wikipédia mais je n'ai pas tout compris , ils prennent un exemple avec cos x = x^3 et il cherche une valeur pour laquelle
f(x)=cosx-x^3 s'annule or ils savent par déduction que le 0 entre 0 et 1 ...
dans mon exemple comment appliquer la méthode de newton ?
merci
- par ptitemimidu18
- 30 Aoû 2008, 16:48
-
- Forum: ✎✎ Lycée
- Sujet: existe t-il une méthode plus rapide ?
- Réponses: 21
- Vues: 1381
Bonjour , Dans un exercice de BAC , on admet que l'équation x\sqrt{x} + x = 5 admet une unique solution alpha sur [1;100]) Donner une valeur approchée à 10^-2 près de alpha ... Alors g(1)=2 g(100)=1100 par tatonnement je trouve à la calculette alpha compris entre [2,05 et 2,06]) comment trouver dire...
- par ptitemimidu18
- 30 Aoû 2008, 16:33
-
- Forum: ✎✎ Lycée
- Sujet: existe t-il une méthode plus rapide ?
- Réponses: 21
- Vues: 1381
oui , je le sais ce n'est pas par rapport à ça que je me posai la question c'est quand on demande les solutions dans C de l'équation (E) c'est les racines ?... Donc je trouve 2 racines complexes : z1 = (-1+i\sqrt{39}) /2 z2 = (-1-i\sqrt{39}) /2 et une solution réelle x=-3 merci!!
- par ptitemimidu18
- 29 Aoû 2008, 20:17
-
- Forum: ✎✎ Lycée
- Sujet: Equations du 3e degré Ts
- Réponses: 9
- Vues: 2503
Bonsoir , On considère l'équation d'inconnue complexe (E) : z^3 + 5z^2+11z+15= 0 1/ Montrer qu'il existe 3 réels tels que pour tout complexe z : z^3+5z^2+11z+15 = (z+3) (az^2+bz+c) donc j'ai développer l'expression de droite je trouve az^3+bz^2+cz+3az^2+3bz+3c soit az^3+z^2 ( 3a+b) +z(b+c)+3c 2/ dét...
- par ptitemimidu18
- 29 Aoû 2008, 19:41
-
- Forum: ✎✎ Lycée
- Sujet: Equations du 3e degré Ts
- Réponses: 9
- Vues: 2503
Bonjour à tous les deux ,
Donc si je comprends bien je pars de f'(x) = 12(x-2)(x^2-1) , je développe et je dois aboutir à ce que j'ai trouvé en dérivant f .
en tout cas , ça marche je retombe sur mes pieds .
merci
- par ptitemimidu18
- 28 Aoû 2008, 10:35
-
- Forum: ✎✎ Lycée
- Sujet: factorisation Ts
- Réponses: 12
- Vues: 763
Bonjour , f est la fonction définie sur R par f(x) = 3x^4-8x^3-6x^2+24x 1/ déterminer les limites de f en {-\infty} et en {+\infty} 2 / déterminer que pour tout réel x , f'(x) = 12 (x-2)(x^2-1) alors pourla 1/ pas de problème la limite en +oo et en -oo est égal à la limite du monome de plus haut deg...
- par ptitemimidu18
- 28 Aoû 2008, 09:58
-
- Forum: ✎✎ Lycée
- Sujet: factorisation Ts
- Réponses: 12
- Vues: 763
Euler911 a écrit:Oui! et comme la limite d'un produit est égale au produit des limites, tu en déduis que
=???)
={-\infty})
- par ptitemimidu18
- 27 Aoû 2008, 14:00
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
compliqué ... mais je vois à près pourquoi
donc ça nous donne
{x}})
et ... je bloque toujours pour la limite
merci
- par ptitemimidu18
- 27 Aoû 2008, 13:45
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
Bien on progresse :D fais attention à la notation: c'est ]-oo,1] et non )-oo;1)! Il y a bien une limite en -oo (et aucune en +oo, ça na pas de sens c. Df) mais elle n'est pas égale à -oo!!! Un premier test le montre : 6$\lim_{-\infty}\left(x+\sqrt{1-x}\right)=-\infty+\sqrt{1-(-\infty�...
- par ptitemimidu18
- 27 Aoû 2008, 13:31
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
Non, non , non et NON!!! :ptdr: pour que \sqrt{1-x} ai un sens il faut que 1-x\geq 0 ! Concentre-toi et vérifie avec des exemples! ok Euler , j'ai amélioré un petit peu ... 1-x\geq 0 donc 1-x > 0 donc -x > -1 donc x < 1 donc D = )-oo;1) donc c'est l'inverse de ce que j'ai dis elle n'est pas définie...
- par ptitemimidu18
- 27 Aoû 2008, 13:06
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
Bonjour , tous le monde ,
j'ai cherché le domaine de définition de la fonction , bien sur c'est (1;+oo( donc si je comprends bien il n'existe pas de limite en -oo car la fonction n'est pas définie ?
merci
- par ptitemimidu18
- 27 Aoû 2008, 12:52
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
Bonjour ,
je bloque pour une limite :
i(x) =
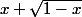
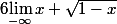
= -oo
et
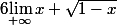
= +oo
est-ce cela ?
merci
- par ptitemimidu18
- 27 Aoû 2008, 09:29
-
- Forum: ✎✎ Lycée
- Sujet: limites Ts
- Réponses: 26
- Vues: 844
Euler911 a écrit:Alors, peut-être qu'une définition de la valeur absolue pourra t'aider:D
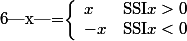
ça va déjà mieux donc lim en -oo = - oo
et lim en + oo = +oo
- par ptitemimidu18
- 26 Aoû 2008, 19:48
-
- Forum: ✎✎ Lycée
- Sujet: vérification limites Ts
- Réponses: 19
- Vues: 1067