1218 résultats trouvés
Revenir à la recherche avancée
Re: Question récurrence forte
Ok pardon, oui j'ai compris. La proposition \forall k<0, P(k) \Rightarrow P(0) est équivalente à P(0) si on convient que \forall k<0, P(k) est vraie. Dans tous les cas on doit bien démontrer P(0) . Je ne parle pas de comment montrer que l'on a P(n) pour un n d...
- 18 Aoû 2022, 12:52
- Forum: ✯✎ Supérieur
- Sujet: Question récurrence forte
- Réponses: 6
- Vues: 726
Re: Question récurrence forte
Soit P(n) une propriété définie sur N, si [∀k < n P(k)] ⇒ P(n) (pour tout n ∈ N) alors P(n) pour tout n ∈ N. Enoncé tel quel ça m'a l'air faux. Il manque en effet l'initialisation. On peut par exemple montrer que pour tout entier n on a n+1<n . L'implication \forall k<n, P(k) \Rightarrow P&...
- 18 Aoû 2022, 12:14
- Forum: ✯✎ Supérieur
- Sujet: Question récurrence forte
- Réponses: 6
- Vues: 726
Re: Irrationalité de e - MPSI / MP
Tu peux écrire 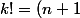!\times (n+2)\dots k) , la fin suivra rapidement.
, la fin suivra rapidement.
- 18 Aoû 2022, 10:45
- Forum: ✯✎ Supérieur
- Sujet: Irrationalité de e - MPSI / MP
- Réponses: 2
- Vues: 567
Re: Les sous-groupes de Z/nZ
ce qui nous amènerait à conclure que les sous-groupes de Z/nZ sont de la forme cl(k) Z/nZ. Je me permets de compléter la réponse de Ben et apporter une précision. La notation cl(k)\mathbb{Z}/n\mathbb{Z} est un peu ambigue. Si cette notation signifie k\mathbb{Z}/n\mathbb{Z} alors je rejoins ...
- 16 Aoû 2022, 21:58
- Forum: ✯✎ Supérieur
- Sujet: Les sous-groupes de Z/nZ
- Réponses: 3
- Vues: 716
Re: Suite arithmétique
lyceen95 a écrit:@Archytas,
Non, on n'a pas :mais :
Donc, pas de Fibonacci, ni de nombre d'or.
La piste que je propose convient tout à fait.
Oups, toutes mes excuses !
- 05 Juil 2022, 11:22
- Forum: ⚜ Salon Mathématique
- Sujet: Suite arithmétique
- Réponses: 5
- Vues: 665
Re: Suite arithmétique
Salut petite question j’ai une suite arithmétique mais avec une raison qui varie de 2 en 2 et je voudrais savoir si avec une formule je peux trouver le nombre de n’importe quel terme imaginons U1= U0 + 10 U2= U1 + 13 U3= U2 +10 U4= U3 +13 U5= U4 +10 …. Es ce que vous auriez une formule pour trouver...
- 03 Juil 2022, 23:16
- Forum: ⚜ Salon Mathématique
- Sujet: Suite arithmétique
- Réponses: 5
- Vues: 665
Re: A la recherche d'entiers
Oui, l'inégalité a l'air compliquée à montrer... je m'y repencherai peut-être quand j'aurai plus de temps si personne n'a trouvé d'ici là. Comment es-tu tombé sur ce problème ?
- 03 Juil 2022, 23:09
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: A la recherche d'entiers
Hmm.. J'ai A3^p=B2^p où A et B sont des entiers. A cause de l'unicité de la décomposition en facteurs premiers, A est forcément un multiple de 2^p , non ? Oui mais -2^p est un multiple de 2^p. Si tu arrives à faire en sorte que de part et d'autre de ton équation les éléments que tu manipules sont d...
- 02 Juil 2022, 10:40
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: A la recherche d'entiers
Si je comprends bien, la contradiction vient du fait que 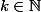 ? Mais je ne comprends pas pourquoi tu peux supposer ça. Le fait que
? Mais je ne comprends pas pourquoi tu peux supposer ça. Le fait que 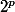 divise
divise 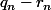 implique seulement qu'il existe
implique seulement qu'il existe 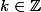 tel que
tel que 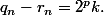
- 01 Juil 2022, 23:17
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: A la recherche d'entiers
Donc \frac{3^p-1}{2^p-1} n'est jamais un entier. Sauf que \frac{3^p-1}{2^p-1} est un entier pour p = 1 :lol: Oui, en effet. Je considère la décomposition en facteurs premiers de n=2^p-1 ce qui sous-entend que n\neq 1 auquel cas \mathbb{Z}/n\mathbb{Z}=\{0\} et l'utilisation du théorème des restes n'...
- 01 Juil 2022, 22:03
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: A la recherche d'entiers
J'ai peut-être une piste. Mais il faut déjà que je démontre que pour p\geq 2, \frac{3^p-1}{2^p-1} n'est pas un entier, histoire de pouvoir ensuite travailler sur des inégalités strictes. A suivre... Je pense avoir trouvé une preuve de ce résultat mais elle est un peu technique. L'idée est de suppos...
- 23 Juin 2022, 19:40
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: A la recherche d'entiers
Intéressant ce problème ! J'arrive seulement à montrer que s'il existe un couple (n,p) qui vérifie les inéquations pour p\geq 2 alors il existe une infinité de couples (n,p) pour des p arbitrairement grands (en montrant qu'il existe un entier dans l'intervalle correspondant à p^s pou...
- 22 Juin 2022, 20:04
- Forum: ⚔ Défis et énigmes
- Sujet: A la recherche d'entiers
- Réponses: 16
- Vues: 1810
Re: Calculer A^n pour n appartient à N.
Oui, my bad. Je pensais que la fonction roots renvoyait toutes les racines même complexes, comme je n'avais que 4 j'ai cru que c'était (x-4)^3.
- 04 Oct 2021, 12:41
- Forum: ✯✎ Supérieur
- Sujet: Calculer A^n pour n appartient à N.
- Réponses: 27
- Vues: 1936
Re: Calculer A^n pour n appartient à n.
Bonsoir, Scinder le polynôme caractéristique suffit, sans qu'il soit besoin de trigonaliser. On a les trois valeurs propres 4,\ 4+2i,\ 4-2i et les projecteurs spectraux correspondants \dfrac14\,A^2-2A+5I_3,\ -\dfrac18\,A^2+\left(1-\dfrac{i}4\right)A-(2-i)I_3,\ -\dfrac18\,A^2+\left&#...
- 04 Oct 2021, 02:02
- Forum: ✯✎ Supérieur
- Sujet: Calculer A^n pour n appartient à N.
- Réponses: 27
- Vues: 1936
Re: Calculer A^n pour n appartient à n.
Tu obtiens quoi comme polynôme caractéristique ?
- 01 Oct 2021, 12:36
- Forum: ✯✎ Supérieur
- Sujet: Calculer A^n pour n appartient à N.
- Réponses: 27
- Vues: 1936
Re: Calculer A^n pour n appartient à n.
Je pense que le mieux est de trigonaliser ta matrice. Pour ça il faut calculer le polynôme caractéristique et ses racines.
- 01 Oct 2021, 12:14
- Forum: ✯✎ Supérieur
- Sujet: Calculer A^n pour n appartient à N.
- Réponses: 27
- Vues: 1936
Re: Polyôme de Legendre
C'est par définition du produit scalaire. Relis l'énoncé de l'exercice.
- 15 Juin 2020, 16:33
- Forum: ✯✎ Supérieur
- Sujet: Polyôme de Legendre
- Réponses: 2
- Vues: 669
Re: Devenir un bon élève.
Faut voir si tu veux être un bon élève et être un ascète. J'imagine que si tu emploies le terme "élève" t'es pas bien vieux. Donc t'es potentiellement dans les meilleures années de ta vie. Commence pas à travailler comme si t'avais 40 piges c'est le meilleur moyen pour devenir un vieux ***...
- 07 Déc 2019, 11:05
- Forum: ☕ Coin café
- Sujet: Devenir un bon élève.
- Réponses: 10
- Vues: 1551
Re: Recherche du point d'inflexion sans l'équation de la cou
Le point d'inflexion est représenté par un changement de monotonie de la pente. Plus précisément sur ton graphe avant d'arriver au point d'inflexion la pente de la tangente est croissante puis elle décroît après le point d'inflexion. Après calculer la pente c'est exactement calculer la dérivée. Donc...
- 04 Juil 2019, 11:09
- Forum: ✯✎ Supérieur
- Sujet: Recherche du point d'inflexion sans l'équation de la courbe
- Réponses: 18
- Vues: 5076
Re: Isomorphisme Explicite
J'ai un peu essayé de fouiller mais sans succès. Je ne vois pas trop comment la théorie des catégorie pourrait nous aider. Je ne m'y connais que très vaguement dans les catégories. Pourrais-tu expliciter un peu ?
- 02 Juil 2019, 20:36
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme Explicite
- Réponses: 2
- Vues: 763
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
