115 résultats trouvés
Revenir à la recherche avancée
- 01 Juin 2007, 14:42
- Forum: ⚔ Défis et énigmes
- Sujet: k^{p-1}=1[p²]
- Réponses: 7
- Vues: 909
Euhh, oui, c'est sans doute ce que je veux dire, mais je ne vois pas ce que l'écriture ultra-formelle apporte.
Les notations c'est bien, mais les raisonnements lisibles ont aussi leur charme...
Les notations c'est bien, mais les raisonnements lisibles ont aussi leur charme...
- 31 Mai 2007, 20:49
- Forum: ⚔ Défis et énigmes
- Sujet: divisibilité par 2000 (facile)
- Réponses: 5
- Vues: 1277
Bonsoir, Je propose de prendre des nombres de la forme 123456789...............0001. Si l'on fait la somme de moins de 1992 tels nombres, l'examen du reste modulo 10000 montre que le nombre obtenu n'est pas divisible par 2000. On peut ensuite regrouper ces nombres en paquets de 1992 comme bon nous s...
- 31 Mai 2007, 19:13
- Forum: ⚔ Défis et énigmes
- Sujet: divisibilité par 2000 (facile)
- Réponses: 5
- Vues: 1277
Il y a beaucoup de solutions
N'oublions pas que les n racines du polynôme que l'on obtient en supprimant les valeurs absolues répondent à la question. De plus, le théorème des valeurs intermédiaires donne une infinité d'autres solutions du moment qu'on a trouvé un point avec l'inégalité stricte comme ça : , ce qui n'est pas dif...
- 29 Mai 2007, 23:49
- Forum: ✯✎ Supérieur
- Sujet: |1+z+...+z^(n-1)|=n|z^n|
- Réponses: 9
- Vues: 693
Ah si !
C'est parce que tous les polynomes symétriques s'écrivent comme polynômes en les polynômes symétriques élémentaires.
Très joli en effet !
C'est parce que tous les polynomes symétriques s'écrivent comme polynômes en les polynômes symétriques élémentaires.
Très joli en effet !
- 24 Mai 2007, 11:25
- Forum: ✯✎ Supérieur
- Sujet: polynome à coeff dans Z
- Réponses: 5
- Vues: 1310
- 24 Mai 2007, 11:00
- Forum: ✯✎ Supérieur
- Sujet: polynome à coeff dans Z
- Réponses: 5
- Vues: 1310
- 22 Mai 2007, 16:00
- Forum: ✯✎ Supérieur
- Sujet: Une égalité récalcitrante
- Réponses: 11
- Vues: 983
- 21 Mai 2007, 23:12
- Forum: ⚖ Place de marché
- Sujet: Gagner de l'argent grâce à son blog ou site internet
- Réponses: 35
- Vues: 3400
Bon, je pose P(\lambda)=1+\lambda+\lambda^2 et \nu=(\lambda\mu)^{-1} . \displaystyle\frac{1}{P(\lambda)}+\frac{1}{P(\mu)}+ \frac{1}{P(\nu)}=\frac{P(\mu)P(\nu)+P(\lambda)P(\nu)+P(\lambda)P(\mu)}{P(\lambda)...
- 21 Mai 2007, 19:01
- Forum: ⚔ Défis et énigmes
- Sujet: salut
- Réponses: 12
- Vues: 1814
Eh bien non, bien sur ! Mais dans le cas d'espèce, si. En effet, comme \lambda et \mu sont supérieurs à 1, \alpha et \beta sont inférieurs à \frac{1}{3} , tandis que (\lambda\mu)^{-1} est inférieur à 1 et \gamma est donc supérieur à \frac{1}{3} . Autrement dit, c'est le plus grand nombre ( z...
- 21 Mai 2007, 14:35
- Forum: ⚔ Défis et énigmes
- Sujet: salut
- Réponses: 12
- Vues: 1814
Bonjour, voici le fruit de mes cogitations : L'inégalité est symétrique en x , y et z . On peut donc supposer que x\leq y\leq z . Posons \lambda=\frac{y}{x}\geq 1 et \mu=\frac{z}{y}\geq 1 . Il s'agit donc de montrer que \displaystyle \frac{x}{1+\lambda+\lambda^2}+\frac{y}{1+\mu+\mu^2}+\frac{z}{1+...
- 21 Mai 2007, 14:13
- Forum: ⚔ Défis et énigmes
- Sujet: salut
- Réponses: 12
- Vues: 1814
Bonsoir.
Laisse nous le temps de réfléchir !!!
Je m'intéresse à ton problème depuis le jour où tu l'as posé, mais je n'ai pas encore trouvé.
Patience ! Reparlons en dans quelques jours...
A bientôt
Laisse nous le temps de réfléchir !!!
Je m'intéresse à ton problème depuis le jour où tu l'as posé, mais je n'ai pas encore trouvé.
Patience ! Reparlons en dans quelques jours...
A bientôt
- 20 Mai 2007, 22:28
- Forum: ⚔ Défis et énigmes
- Sujet: salut
- Réponses: 12
- Vues: 1814
Indicatrice d'Euler
Bonsoir à tous, un petit dernier avant d'aller au lit :
Soit un entier naturel différent de 3 tel que
un entier naturel différent de 3 tel que \mid n-1) . Montrer que
. Montrer que  n'est pas un multiple de 3.
n'est pas un multiple de 3.
Soit
- 19 Mai 2007, 21:01
- Forum: ⚔ Défis et énigmes
- Sujet: Indicatrice d'Euler
- Réponses: 1
- Vues: 787
- 19 Mai 2007, 20:47
- Forum: ⚔ Défis et énigmes
- Sujet: p-diviseurs
- Réponses: 4
- Vues: 1064
S'il y a deux facteurs supérieurs à 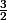 , tous les autres étant supérieurs à 1, le produit est supérieur à
, tous les autres étant supérieurs à 1, le produit est supérieur à 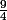 .
.
- 14 Mai 2007, 13:58
- Forum: ⚔ Défis et énigmes
- Sujet: unicité
- Réponses: 18
- Vues: 1517
Mon dieu que c'est compliqué !!! Aviateurpilot est parti dans la stratosphère ! Prenons un a entier naturel. \displaystyle \frac{2a+1}{a+1}=2-\frac{1}{a+1} Ce quotient est égal à 1 si a=0 et est supérieur à \displaystyle \frac{3}{2} si a \neq 0 . Si plus d'un des a_i est non nul, le produit des quot...
- 13 Mai 2007, 22:25
- Forum: ⚔ Défis et énigmes
- Sujet: unicité
- Réponses: 18
- Vues: 1517
Bonsoir, En fait, il y a deux choses bien différentes. Le fait que les seuls corps quadratiques imaginaires qui ont un nombre de classes égal à un sont ceux qui sont cités dans cet article est un théorème difficile et complètement indépendant de ton exercice. Le fait qu'un n comme celui de l'exercic...
- 04 Mai 2007, 22:52
- Forum: ⚔ Défis et énigmes
- Sujet: arithmetique :)
- Réponses: 19
- Vues: 2302
Bonjour à tous. L'erreur d'énoncé est d'autant plus regrettable que tout le début de la discussion a été consacré à la clarification du dit énoncé. Quand je pense à toutes ces heures passées à essayer de franchir la frontière entre \sqrt[3]{n} et \sqrt{n} ! Tous les angles d'attaque ramenaient à cet...
- 03 Mai 2007, 22:53
- Forum: ⚔ Défis et énigmes
- Sujet: arithmetique :)
- Réponses: 19
- Vues: 2302
Bonjour à tous. Après beaucoup d'efforts, j'arrive à montrer que pour k \leq n-2 , si k^2+k+n n'est pas premier, alors il a exactement deux facteurs premiers, tous deux supérieurs à k . De plus, s'il existe un tel k , il doit en exister au moins trois. Mais je n'arrive pas à aller plus loin. Je sera...
- 28 Avr 2007, 13:34
- Forum: ⚔ Défis et énigmes
- Sujet: arithmetique :)
- Réponses: 19
- Vues: 2302
Bonjour chers amis,
Une petite précision sur la formulation d'aviateurpilot :
il faut inclure 0 dans les intervalles. Autrement dit, n lui-même doit être premier.
Sinon, 77 est un contre-exemple.
A bientôt (avec une solution j'espère...)
Une petite précision sur la formulation d'aviateurpilot :
il faut inclure 0 dans les intervalles. Autrement dit, n lui-même doit être premier.
Sinon, 77 est un contre-exemple.
A bientôt (avec une solution j'espère...)
- 22 Avr 2007, 17:55
- Forum: ⚔ Défis et énigmes
- Sujet: arithmetique :)
- Réponses: 19
- Vues: 2302
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
