Arithmetique :)

[namfoodle sheppen]

un beau petit exo d'arithmetique pour dynamiser un peu le forum d'olympiade :happy2: : soit n un entier tel que k²+k+n soit premier pour k

[Thalès]

on peut démontrer ça, si on prouve que : n-2> racine cubique de n et puisque racine cubique de n > k donc : n-2> k où k²+k+n est premier mais l'inégalité : n-2> racine cubique de n n'est juste que lorsque n est plus grand ou égal à 4, déjà on peut dire que n est différent de 0 car si ça été le cas on aura : k²+k+0 = k(k+1) donc il ne sera pas premier , en gros le n ne va pas être un multiple ou un diviseur de k pour la primalité du k²+k+n.
Précise nous s'il te plait l'ensemble où le k appartient car tu n'as pas donné de précision sur ce nombre :), merci.
++

[yos]

Bonsoir.
Les petits n sont sans intérêt. L'inégalité est tout à fait triviale.
Du coup, savoir que k²+k+n est premier jusqu'à est moins fort (en apparence en tout cas) que savoir que k²+k+n est premier jusqu'à n-2.
Bref il me semble, Thalès que tu passes à côté de l'exercice.

[Thalès]

Moi j'ai juste proposé un chemin qui permet de démontrer
Si on a k²+k+n premier pour k racine cubique de n , et d'après les calculs que j'ai fait , l'égalité est juste pour n>4, donc je pense que c'est le bon chemin.

Savoir que k²+k+n est premier jusqu'à racine cubique de n est moins fort (en apparence en tout cas) que savoir que k²+k+n est premier jusqu'à n-2.

Je suis d'accord, mais là tu as k²+k+n pour "k" qui est plus petit que racine cubique de n , et tu dois démontrer que l'expression marche pour le "k" qui est plus petit que n-2, c'est différent c'est comme si on as k premier pour 3<6 et on dois démontrer que k premier pour 3<9, et toi tu dis que k premier pour 6 est moins fort que k premier pour 9, c'est juste mais quel rapport avec l'exercice? aucun, donc en fin de compte c'est toi Yos qui est à coté de la plaque, lis bien l'exercice.
Puis, pour démontrer l'exercice, il faut que k soit un entier alors que Namfoodle Sheppen ne l'as même pas précisé dans l'énoncé, puis si il est pair ou impair, je pense qu'il y a une hypothèse qui manque et qui nous permettra pas de trouver une solution à la question posée, c'est à Namfoodle Sheppen de revoir son énoncé.

[BiZi]

Merci pour ces intéressantes précisions, j'espère que tout est clair maintenant yos?

:briques:

[yos]

Merci pour ces intéressantes précisions, j'espère que tout est clair maintenant yos?

Salut Bizi. C'est toi qui devrait être plus clair.

[aviateurpilot]

[quote="namfoodle sheppen"]un beau petit exo d'arithmetique pour dynamiser un peu le forum d'olympiade :happy2: : soit n un entier tel que k²+k+n soit premier pour k

[Thalès]

Ok c'est bon

[namfoodle sheppen]

oui aviateur pilot a remis les choses aux clair et en format latex pour moi merci :happy2: . Maintenant il ne reste plus qu'à le résoudre ...

[redwolf]

Bonjour chers amis,

Une petite précision sur la formulation d'aviateurpilot :

il faut inclure 0 dans les intervalles. Autrement dit, n lui-même doit être premier.
Sinon, 77 est un contre-exemple.

A bientôt (avec une solution j'espère...)

[redwolf]

Bonjour à tous.

Après beaucoup d'efforts, j'arrive à montrer que pour , si n'est pas premier, alors il a exactement deux facteurs premiers, tous deux supérieurs à . De plus, s'il existe un tel , il doit en exister au moins trois.

Mais je n'arrive pas à aller plus loin. Je serais enchanté de lire une solution. Namfoodle sheppen, pourrais-tu m'envoyer la tienne ? Merci.

[BiZi]

Bonjour à tous.

Après beaucoup d'efforts, j'arrive à montrer que pour , si n'est pas premier, alors il a exactement deux facteurs premiers, tous deux supérieurs à . De plus, s'il existe un tel , il doit en exister au moins trois.

Mais je n'arrive pas à aller plus loin. Je serais enchanté de lire une solution. Namfoodle sheppen, pourrais-tu m'envoyer la tienne ? Merci.

yay! j'ai trouvé la même chose

[namfoodle sheppen]

ce n'est pas la mienne, je ne l'avais pas trouvé. Cet exercice est extrait d'un bouquin d'exo d'olympiade de Paul Bourgade édité chez cassini pour ceux que ça interesse. Je l'avais mis sur ce forum parce que c'est le premier énoncé que je vois où on arrive ainsi à générer des nombres premiers. Voici la solution :
==> solution par l'absurde :"on suppose qu'il existe l qui vérifie les conditions de l'énoncé. On le choisit minimal. Soit q le plus petit diviseur premier de l^2+l+n. Alors q<=2l (verification par l'absurde). Comme q<=2l on peut l'écrire l-k ou l+k+1 avec 0<=k<=l-1. Or comme (l^2+l+n)-(k^2+k+n)=(l-k)(l+k+1) q divise également k^2+k+n. Or comme l a ete choisi comme minimal, et q est premier, on a forcement q=k^2+k+n.
Comme q^2<=l^2+l+n , (k^2+k+n)^2<=(n-2)^2+(n-2)+n=n^2-2n+2 ce qui est absurde."

[namfoodle sheppen]

euh d'ailleurs en voyant l'enonce que je vous avais donné c pour l<=racine (n/3) et non l<=racine cubique(n).
je suis vraiment désolé === >> :briques:

[BiZi]

euh d'ailleurs en voyant l'enonce que je vous avais donné c pour l> :briques:

.....................................................................................

Je DETESTE ce genre d'erreur :briques:

[namfoodle sheppen]

bah bizi je suis vraiment desole ... ecoute si tu veux on peut se voir pour que je te console. Ca depend t'habites ou ?

[redwolf]

Bonjour à tous.

L'erreur d'énoncé est d'autant plus regrettable que tout le début de la discussion a été consacré à la clarification du dit énoncé.
Quand je pense à toutes ces heures passées à essayer de franchir la frontière entre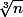 et 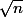! Tous les angles d'attaque ramenaient à cette différence...

Quant à "générer des nombres premiers", cet enoncé ne le permet en aucun cas. En effet, il est prouvé que 41 est le plus grand entier pour lequel la conclusion de l'énoncé est vérifiée. Je vous renvoie à cette page pour quelques détails. Inutile donc d'espérer dépasser 1601 par cette méthode !

[namfoodle sheppen]

merci de la précision redwolf tu saurais pas ou on pourrait trouver une démonstration de la limitation de cette proriété aux nombres de heegner ?

[redwolf]

Bonsoir,

En fait, il y a deux choses bien différentes.
Le fait que les seuls corps quadratiques imaginaires qui ont un nombre de classes égal à un sont ceux qui sont cités dans cet article est un théorème difficile et complètement indépendant de ton exercice.

Le fait qu'un comme celui de l'exercice vérifie que a un nombre de classes égal à 1 est sans doute plus facile (même si je n'en sais rien dans le fond...) et je propose d'y réfléchir un petit peu. J'essaierai de trouver une référence si aucun d'entre nous ne trouve d'idée.

[namfoodle sheppen]

pour la deuxieme en effet j'ai trouve une démonstration dans "invitation au monde de fermat wiles" de hellegouarch. Par contre je cherche la demo pour les nombre de heegner. Mais impossible de la trouver en francais ou en anglais :triste: