Voilà, tout est quasiment dans le titre:
sous quelles conditions a-t-on: |1+z+...+z^(n-1)|=n|z^n| ? ( z complexe)
Je sais que |u+v|=|u|+|v| ssi u=µv avec µ réel positif, et que cette dernière proposition se généralise à n termes, mais je n'arrive pas à résoudre celle de mon titre.
Est-ce que quelqu'un pourrait m'aiguiller pour cette démonstration ( faut il se servir de |u+v|=|u|+|v|) ?
Merci
|1+z+...+z^(n-1)|=n|z^n|
10 messages
- Page 1 sur 1
"Yos" a écrit:Une solution de module 1 (z=e^{it}) donnerait sin nt = nsin t ...
Je n'arrive pas tout à fait à ce résultat:
On a:
d'où:
pour
or ,
D'où:
PS: je viens juste de me mettre à LaTex (pour rendre ce post lisible), c'est excellent ce truc !!
Il y a beaucoup de solutions
N'oublions pas que les  racines du polynôme que l'on obtient en supprimant les valeurs absolues répondent à la question.
racines du polynôme que l'on obtient en supprimant les valeurs absolues répondent à la question.
De plus, le théorème des valeurs intermédiaires donne une infinité d'autres solutions du moment qu'on a trouvé un point avec l'inégalité stricte comme ça : , ce qui n'est pas difficile.
Pour , on obtient une belle courbe que l'on peut décrire assez explicitement.
, on obtient une belle courbe que l'on peut décrire assez explicitement.
Quand croit, on obtient une courbe de solutions qui se tasse sur le cercle unité. La seule solution qui convient pour tout
croit, on obtient une courbe de solutions qui se tasse sur le cercle unité. La seule solution qui convient pour tout  est
est 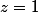 .
.
De plus, le théorème des valeurs intermédiaires donne une infinité d'autres solutions du moment qu'on a trouvé un point avec l'inégalité stricte comme ça : , ce qui n'est pas difficile.
Pour
Quand
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
